Траектория перемещения материальной точки - понятие, которое используется в физике для описания пути, который проходит точка при перемещении в пространстве. Это понятие является одним из основных в физике и может быть применено к различным объектам и системам.
Точка представляет собой объект, у которого нет размеров и формы, а перемещение точки может происходить в трех измерениях - по горизонтали, вертикали и вдоль оси времени. Траектория точки может быть прямой, кривой или иметь сложную форму.
Траектория является важным понятием при изучении физических законов движения и позволяет установить связь между путем, который проходит объект, и временем требуемым для этого перемещения. Понимание траектории позволяет предсказывать движение объектов и определять характеристики их движения, такие как скорость,加速度 и т.д.
Таким образом, траектория перемещения материальной точки играет важную роль в физике, позволяя описывать и анализировать движение объектов в пространстве и времени.
Определение траектории
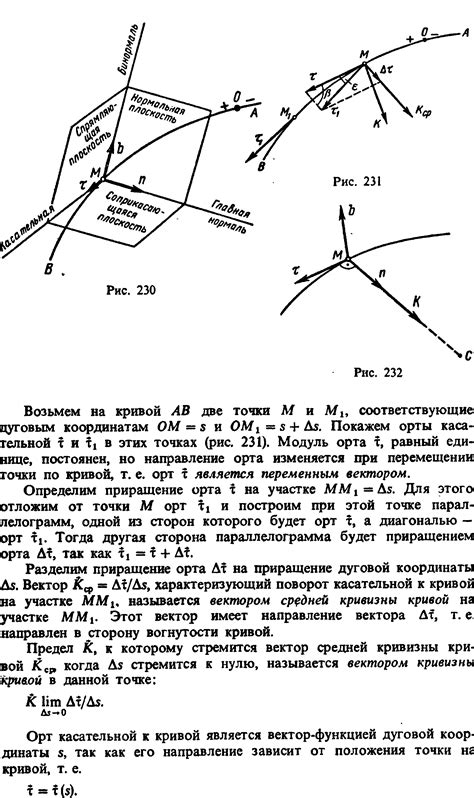
Для определения траектории необходимо знать положение материальной точки в разные моменты времени. Эти данные могут быть представлены в виде координат точки или ее вектора перемещения. Зная положение точки в начальный момент времени и ее скорость или ускорение, можно определить, какая траектория будет описана в результате ее движения.
Траектория может быть прямолинейной, если скорость и направление движения материальной точки постоянны, или иметь сложную форму, если эти параметры изменяются во времени. Например, если материальная точка движется по круговой траектории с постоянной скоростью, ее траектория будет окружностью.
Определение траектории играет важную роль в физике, механике и других науках. Изучение траекторий позволяет описывать и предсказывать движение объектов, а также анализировать влияние различных факторов на их траектории.
| Примеры траекторий | Краткое описание |
|---|---|
| Прямая линия | Материальная точка движется прямолинейно на одной оси. |
| Окружность | Материальная точка движется по окружности с постоянной скоростью. |
| Парабола | Материальная точка движется по параболической траектории под действием гравитации. |
Траектория и способы ее определения
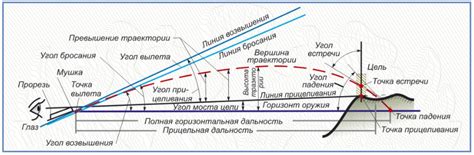
Траектория представляет собой путь, по которому перемещается материальная точка в пространстве или на плоскости. Определение траектории играет важную роль в физике, механике, астрономии и других науках, где изучается движение тел.
Существует несколько способов определения траектории. Один из них - наблюдение за движением объекта и отслеживание его положения в пространстве на протяжении определенного времени. С помощью этого метода можно получить достаточно точные данные о траектории, особенно если через определенные промежутки времени фиксировать положение точки.
Другим способом является математическое моделирование движения. Зная начальные условия и применяя уравнения, описывающие данное движение, можно вычислить траекторию точки. Этот метод позволяет определить траекторию с большой точностью, но требует знания математических методов и навыков.
Также существует возможность определить траекторию с помощью экспериментальных исследований. Например, путем измерения силы тяжести или анализа сил, действующих на объект при движении, можно определить форму и характер траектории.
Определение траектории перемещения материальной точки является важным элементом изучения движения объектов в пространстве. Различные методы позволяют получить разные уровни точности и степень детализации траектории, что позволяет более полно и точно описывать движение объектов и использовать полученную информацию в научных и инженерных расчетах.
Расчёт траектории при равномерном движении

Для расчёта траектории материальной точки при равномерном движении необходимо знать ее начальное положение, скорость и время движения. Начальное положение можно задать координатами (x₀, y₀) или радиус-вектором R₀. Скорость можно определить по модулю v и углу α, при этом угол α равен углу между скоростью и осью x. Время движения обозначим как t.
Если движение материальной точки прямолинейное, то траектория будет являться прямой линией. Если движение криволинейное, то траектория может быть задана уравнением кривой, например, окружностью.
Для определения траектории перемещения материальной точки при равномерном движении можно воспользоваться следующими формулами:
| Тип траектории | Формула траектории |
|---|---|
| Прямолинейное движение | x = x₀ + v * t |
| Движение по окружности | x = x₀ + R * cos(α) * (1 - cos(ω * t)) |
Где:
- x – координата точки по оси x на траектории;
- x₀ – начальная координата точки по оси x;
- v – скорость материальной точки;
- t – время движения;
- R – радиус окружности траектории;
- α – угол между скоростью и осью x;
- ω – угловая скорость движения по окружности.
Используя данные формулы, можно рассчитать траекторию перемещения материальной точки при равномерном движении и определить ее положение в любой момент времени.
Криволинейное движение и его траектория
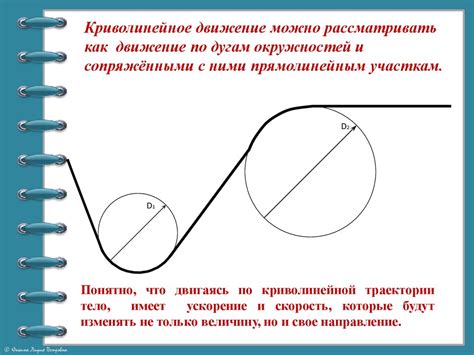
Траектория криволинейного движения представляет собой геометрическую кривую, которая отображает путь, пройденный материальной точкой. Траектория может быть простой, например, прямой линией или окружностью, или же сложной, как, например, эллипс или спираль.
Траектория криволинейного движения может быть определена с помощью математических функций, таких как функция зависимости координат точки от времени. Такие функции позволяют описать форму и направление траектории. Например, для прямолинейного движения можно использовать функцию прямой линии, а для кругового движения - функцию окружности.
Изучение криволинейного движения и его траектории имеет большое значение в физике и инженерии. Оно позволяет предсказать и анализировать движение различных тел и частиц, а также дает возможность оптимизировать траекторию движения в различных приложениях, например, в авиации, робототехнике или автомобильной промышленности.
Влияние факторов на форму траектории
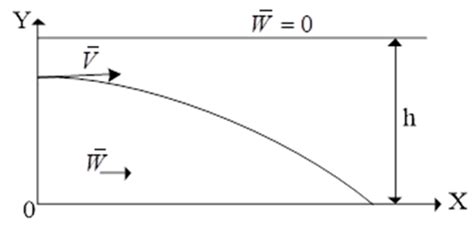
Форма траектории перемещения материальной точки может быть различной и зависит от разных факторов. Влияние этих факторов на форму траектории может быть исследовано и описано с помощью математических моделей и экспериментов.
Одним из факторов, влияющих на форму траектории, является сила, действующая на материальную точку. Если сила равномерна по величине и направлению, то траектория будет являться прямой линией. Если сила меняется по величине и/или направлению, то траектория может иметь сложную кривизну.
Еще одним фактором, влияющим на форму траектории, является начальная скорость материальной точки. Если начальная скорость равна нулю, то траектория будет состоять из одной точки – самой точки начального положения. Если начальная скорость ненулевая, то траектория будет иметь форму ломаной линии или кривой, в зависимости от изменения скорости.
Также форму траектории может влиять наличие препятствий или препятствующих факторов на пути движения материальной точки. Если препятствий нет, то траектория будет определяться только воздействием сил и начальной скорости. Если же есть препятствия, то траектория может быть изменена в силу столкновений или отражений от препятствий.
| Факторы, влияющие на форму траектории | Описание влияния |
|---|---|
| Сила | Если сила равномерна – прямая линия, если меняется – кривизна |
| Начальная скорость | Равна нулю - одна точка, ненулевая - ломаная линия или кривая |
| Препятствия | Могут изменять траекторию через столкновения или отражения |
Применение знания о траектории в реальной жизни

1. Физика и механика: В физике и механике знание о траектории необходимо для анализа и предсказания движения объектов. Например, при моделировании движения тела в пространстве, знание о его траектории позволяет определить его физические характеристики. Траектория также используется в физических экспериментах и приложениях, таких как разработка и тестирование ракет и самолетов.
2. Геодезия и навигация: Геодезия использует знание о траектории для определения и измерения точек на Земле. Траектория может использоваться для создания карт, навигации в режиме реального времени, такой как GPS, определения границ земельных участков и местоположения объектов на местности.
3. Спорт: В спорте знание о траектории позволяет тренерам и игрокам анализировать и улучшать технику и стратегию игры. Например, в гольфе знание о траектории мяча помогает гольфистам выбрать правильный угол удара и силу для достижения желаемого результата.
4. Автомобильная промышленность: В автомобильной промышленности знание о траектории используется при разработке безопасных и эффективных автомобилей. Инженеры и конструкторы используют знание о траектории для создания оптимальных тормозных систем, управления устойчивостью и других систем, которые обеспечивают корректное поведение автомобиля во время движения.
Все эти примеры показывают, как знание о траектории перемещения материальной точки играет важную роль в различных областях нашей жизни. Оно помогает нам лучше понять и контролировать движение объектов, повышая безопасность, эффективность и точность в различных сферах деятельности.



