Средняя скорость движения - одна из основных физических характеристик движения. Она определяется как отношение пройденного пути к затраченному на это время. Средняя скорость измеряется в единицах длины, например метрах или километрах, и единицах времени, как секундах или часах.
Средняя скорость может быть постоянной или изменяться в зависимости от времени. При постоянной скорости путь, пройденный за равные промежутки времени, одинаков, а на графике зависимости пути от времени видна прямолинейная зависимость.
Примером постоянной скорости является скорость равномерного движения, когда тело перемещается по прямой с одинаковой скоростью. В этом случае средняя скорость равна скорости тела и не зависит от времени движения.
Средняя скорость движения в физике: определение и принципы

Для определения средней скорости движения необходимо учитывать два фактора: пройденное расстояние и время, затраченное на это движение. Пройденное расстояние измеряется в метрах (м), а время – в секундах (с), минутах (мин) или часах (ч).
Когда тело движется равномерно, то его средняя скорость рассчитывается по формуле:
Средняя скорость (V) = Пройденный путь (S) / Время (t)
Пример: если автомобиль проехал 300 км за 5 часов, то средняя скорость движения будет равна:
V = 300 км / 5 ч = 60 км/ч
Величина средней скорости может быть положительной, отрицательной или нулевой. Положительная скорость указывает на движение в положительном направлении, отрицательная – в отрицательном, а нулевая – на отсутствие движения.
Важно отличать среднюю скорость от мгновенной. Мгновенная скорость показывает скорость движения в каждый отдельный момент времени и рассчитывается по производной от зависимости пройденного пути от времени.
Средняя скорость – основной параметр для изучения движения тела и широко применяется в различных физических задачах. Также ее понятие важно для понимания других основных понятий физики, таких как ускорение, равномерное движение и перемещение.
Итак, средняя скорость движения – это отношение пройденного пути к времени, затраченному на это движение. Понятие средней скорости является важным для изучения движения тела и находит свое применение в различных физических задачах.
Расчет средней скорости движения в физике

Формула для расчета средней скорости выглядит следующим образом:
v = ∆s / ∆t
где v – средняя скорость движения, ∆s – пройденный путь, и ∆t – затраченное время.
Если объект движется с постоянной скоростью, то средняя скорость будет равна его инстантной скорости. Если объект движется с переменной скоростью, то среднюю скорость можно рассчитать, разделив пройденный путь на затраченное время.
Например, пусть объект пройдет расстояние 100 м за время 10 секунд. Тогда средняя скорость будет равна 10 м/с:
v = 100 м / 10 с = 10 м/с
Расчет средней скорости помогает определить, насколько быстро движется объект, а также сравнить скорости различных объектов. Это важное понятие в физике, которое используется для анализа и описания движения тел и процессов.
Формула расчета средней скорости

Средняя скорость движения можно определить с помощью простой формулы:
Средняя скорость = пройденное расстояние / время движения
Для расчета средней скорости необходимо знать пройденное расстояние и время, затраченное на это движение.
Пройденное расстояние обычно измеряется в метрах или километрах, а время движения – в секундах, минутах или часах. Результат выражается в метрах в секунду (м/с), километрах в час (км/ч) или других единицах измерения скорости.
Например, если объект прошел расстояние в 100 метров за 10 секунд, средняя скорость будет равна:
Средняя скорость = 100 м / 10 сек = 10 м/с
Формула расчета средней скорости позволяет определить изменение положения объекта за определенный промежуток времени и является одной из основных концепций в физике.
Отличие средней скорости от мгновенной скорости

Средняя скорость - это отношение пройденного пути к времени, за которое это путешествие было совершено. Она рассчитывается по формуле V = S ÷ t, где V - средняя скорость, S - путь, пройденный телом, и t - время, за которое пройден этот путь. Средняя скорость позволяет узнать, с какой средней скоростью тело перемещается относительно начальной и конечной точек.
Мгновенная скорость, с другой стороны, является мгновенным значением скорости в определенный момент времени. Это скорость, которую тело имеет в данный момент времени. Для вычисления мгновенной скорости нам нужно знать аналитическую функцию, описывающую движение тела. Мгновенная скорость может быть разная в разные моменты времени, поскольку тело может двигаться с разной скоростью или менять направление движения.
Для лучшего понимания отличия между средней и мгновенной скоростью, рассмотрим следующий пример. Представим, что тело движется по прямой, с начальной точкой A и конечной точкой B. Если мы хотим вычислить среднюю скорость движения этого тела, мы измеряем время, за которое оно прошло расстояние между А и В, и делим на это время. Это дает нам среднюю скорость во всем пути от А до В.
С другой стороны, мгновенная скорость дает нам скорость тела в каждой точке его пути от А до В. Например, если тело движется с ускорением или замедляет перед достижением точки В, его мгновенная скорость в разных точках будет разной.
Таким образом, отличие между средней скоростью и мгновенной скоростью заключается в том, что средняя скорость представляет собой среднее значение скорости за все путешествие, тогда как мгновенная скорость показывает скорость в определенный момент времени или в определенной точке.
Значение средней скорости в изучении движения

Средняя скорость позволяет оценить, с какой интенсивностью тело перемещается в пространстве за определенное время. Она определяет среднюю скорость изменения положения тела в единицу времени.
Средняя скорость также может использоваться для оценки изменения скорости с течением времени. Если скорость тела остается постоянной в течение определенного интервала времени, средняя скорость будет равна мгновенной скорости.
Значение средней скорости позволяет сравнивать движения разных тел и определить, какое из них движется быстрее или медленнее. Средняя скорость также может использоваться для расчета времени, необходимого для преодоления определенной дистанции, и для прогнозирования приближения или удаления тела от точки отсчета.
Важно понимать, что средняя скорость может быть разной для разных участков движения тела. Также она может меняться во времени, если скорость тела не постоянна.
Средняя скорость является фундаментальной величиной в физике и находит широкое применение в различных областях науки и техники, включая механику, астрономию, физику твердого тела и другие.
Зависимость средней скорости от времени и пройденного пути
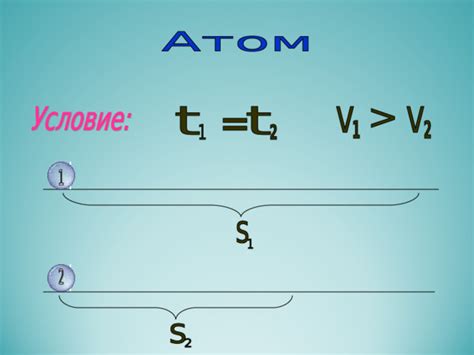
Средняя скорость движения может изменяться в зависимости от времени и пройденного пути. Это объясняется тем, что средняя скорость рассчитывается как отношение пройденного пути к затраченному времени.
Если движение происходит с постоянной скоростью, то средняя скорость будет постоянной и не зависит от времени и пройденного пути. В этом случае формула для расчета средней скорости принимает вид:
средняя скорость = пройденный путь / затраченное время
Однако в реальных условиях движение может быть переменным. Например, движение автомобиля в городе может происходить с разной скоростью на разных участках дороги или в разное время суток.
Когда скорость движения меняется, средняя скорость будет различаться в зависимости от времени и пройденного пути. Если за фиксированный промежуток времени автомобиль прошел одно и то же расстояние, то средняя скорость будет выше в те моменты времени, когда автомобиль движется быстрее, и ниже в те моменты времени, когда автомобиль движется медленнее.
Таким образом, средняя скорость зависит от соотношения времени и пройденного пути во время движения. Чем больше пройденное расстояние при фиксированном времени, тем выше средняя скорость. Аналогично, чем меньше пройденное расстояние при фиксированном времени, тем ниже средняя скорость.
Примеры расчета средней скорости в различных ситуациях

Пример 1:
Пусть объект движется прямолинейно на 500 метров за время 10 секунд. Чтобы найти среднюю скорость, мы делим пройденное расстояние на затраченное время.
Средняя скорость = пройденное расстояние / затраченное время
Средняя скорость = 500 м / 10 с = 50 м/с
Пример 2:
Представим ситуацию, когда объект движется с разной скоростью в течение пути. Пусть он сначала движется со скоростью 20 м/с, затем со скоростью 30 м/с и, наконец, со скоростью 40 м/с. Чтобы найти среднюю скорость, мы суммируем пройденное расстояние и делим на затраченное время.
Средняя скорость = пройденное расстояние / затраченное время
Средняя скорость = (20 м/с + 30 м/с + 40 м/с) / 3 = 90 м/с / 3 = 30 м/с
Пример 3:
Рассмотрим случай, когда объект движется с постоянной скоростью в одном направлении, а затем возвращается обратно той же скоростью. Пусть объект движется 200 метров вперед со скоростью 10 м/с, а затем возвращается назад на ту же дистанцию со скоростью 10 м/с. Чтобы найти среднюю скорость, мы суммируем пройденное расстояние и делим на затраченное время.
Средняя скорость = пройденное расстояние / затраченное время
Средняя скорость = (200 м + 200 м) / (10 с + 10 с) = 400 м / 20 с = 20 м/с
Таким образом, расчет средней скорости зависит от данных о пройденном расстоянии и затраченном времени, а также от условий движения объекта.
Практическое применение средней скорости в жизни

Средняя скорость, определенная как отношение пройденного пути к затраченному времени, имеет широкое практическое применение в жизни. Рассмотрим несколько сфер, где средняя скорость играет ключевую роль.
| Сфера | Пример применения средней скорости |
|---|---|
| Транспорт | При планировании маршрута поездки на машине, знание средней скорости позволяет оценить время, необходимое для достижения цели и выбрать оптимальный путь. |
| Спорт | В спорте средняя скорость является важным показателем. Например, в беге на длинные дистанции знание средней скорости позволяет спортсмену контролировать свои усилия и распределить энергию на протяжении всей дистанции. |
| Экономика | В экономике средняя скорость используется для оценки эффективности работы процессов и систем. Например, при расчете производительности производственной линии важно знать среднюю скорость производства. |
| Путешествия | При планировании путешествия с использованием общественного транспорта или самолета знание средней скорости позволяет оценить время, необходимое для перемещения между городами или странами. |
Это всего лишь несколько примеров, но они показывают, что средняя скорость имеет практическую значимость во многих сферах жизни. Понимание и умение использовать среднюю скорость позволяют планировать и прогнозировать результаты различных процессов и задач, что делает ее важным понятием в физике и повседневной жизни.



