Среднеарифметическое число – это один из основных понятий, которые изучают в школьном курсе математики. В шестом классе ученики начинают углубленно изучать арифметические операции, в том числе и среднеарифметическое.
Среднеарифметическое число позволяет найти среднее значение ряда чисел. Для его вычисления необходимо сложить все числа ряда и разделить их на их количество. Например, если у нас есть ряд чисел: 5, 7, 10, 12, то чтобы найти среднеарифметическое число, нужно сложить эти числа (5 + 7 + 10 + 12 = 34) и разделить на их количество (34 / 4 = 8,5). Таким образом, среднеарифметическое число для данного ряда равно 8,5.
Среднеарифметическое число позволяет нам получить общую информацию о ряде чисел, показывая нам их среднее значение. Оно также может быть использовано для сравнения значений различных рядов чисел и определения их сходства или различия. Важно понимать, что среднеарифметическое число не всегда представляет одно из чисел ряда, оно может быть как больше, так и меньше чисел в ряду.
В 6 классе ученики изучают различные методы вычисления среднеарифметического числа, а также узнают, как применять его в решении задач. Это важное понятие помогает развивать математическую логику и абстрактное мышление учащихся.
Среднеарифметическое число: определение и примеры
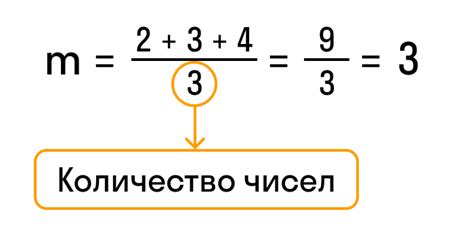
Для вычисления среднеарифметического числа нужно выполнить следующие шаги:
- Сложить все числа в наборе.
- Поделить полученную сумму на количество чисел в наборе.
Давайте рассмотрим пример для лучшего понимания:
У нас есть следующий набор чисел: 5, 8, 4, 2, 7.
Сначала сложим эти числа: 5 + 8 + 4 + 2 + 7 = 26.
Затем поделим полученную сумму на количество чисел в наборе, в данном случае это 5: 26 / 5 = 5.2.
Таким образом, среднеарифметическое число для данного набора чисел равно 5.2.
Среднеарифметическое число помогает сделать обобщение данных и получить общую информацию о наборе чисел. Оно может использоваться для сравнения различных наборов чисел и анализа статистических данных.
Определение среднеарифметического числа

Для вычисления среднеарифметического числа нужно следовать нескольким шагам:
- Суммируйте все числа в наборе.
- Подсчитайте количество чисел в наборе.
- Разделите полученную сумму на количество чисел в наборе.
Таким образом, среднеарифметическое число позволяет найти среднее значение набора чисел и упростить его представление. Это полезное понятие в математике, которое позволяет анализировать и сравнивать различные данные.
Давайте рассмотрим пример:
| Числа | Сумма | Количество | Среднеарифметическое число |
|---|---|---|---|
| 5, 8, 11 | 24 | 3 | 8 |
В данном примере мы имеем набор чисел 5, 8 и 11. Для нахождения среднеарифметического числа мы суммируем эти числа (5 + 8 + 11 = 24) и делим полученную сумму на количество чисел в наборе (24 / 3 = 8). Таким образом, среднеарифметическое число для данного набора чисел равно 8.
Среднеарифметическое число является одним из базовых понятий в математике и широко применяется при анализе данных и решении различных задач. Оно позволяет упростить представление набора чисел и сравнивать их между собой.
Как найти среднеарифметическое число
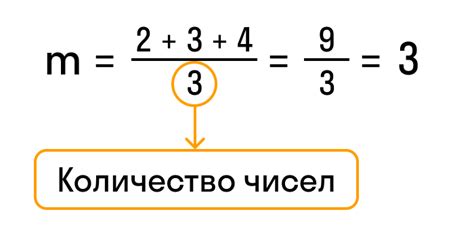
Для нахождения среднеарифметического числа вы должны выполнить следующие шаги:
- Составьте список чисел, для которых вы хотите найти среднее.
- Сложите все числа из списка, чтобы получить их сумму.
- Разделите полученную сумму на количество чисел в списке.
Рассмотрим пример:
| Число | Сумма |
|---|---|
| 3 | 3 |
| 5 | 8 |
| 7 | 15 |
Сначала сложим числа: 3 + 5 + 7 = 15. Затем разделим сумму на количество чисел в списке: 15 / 3 = 5. Таким образом, среднеарифметическое число для этого набора чисел равно 5.
Теперь вы знаете, как найти среднеарифметическое число! Этот метод может быть полезен, когда вам нужно найти среднее значение для большого набора чисел.
Примеры использования среднеарифметического числа в математике
1. Статистика:
Среднеарифметическое число используется для нахождения среднего значения в наборе данных. Например, если у нас есть набор чисел: 4, 5, 6, 7, 8, то среднеарифметическое число будет равно (4+5+6+7+8)/5 = 6.
2. Усреднение:
Среднеарифметическое число используется для усреднения значений. Например, если у нас есть несколько оценок по математике: 5, 4, 3, 2, 5, то среднеарифметическое число покажет какая средняя оценка у ученика.
3. Финансы:
Среднеарифметическое число может использоваться в финансовых расчетах. Например, для определения средней зарплаты в компании или среднего уровня рентабельности.
4. Нахождение недостающих значений:
Среднеарифметическое число может использоваться для нахождения недостающих значений в наборе данных. Например, если у нас есть набор чисел: 2, 4, 6, X, то мы можем использовать среднеарифметическое число, чтобы найти значение X.
Среднеарифметическое число является мощным инструментом в математике и может быть использовано во многих различных ситуациях. Оно помогает нам оценить среднее значение и упростить сложные расчеты.



