Сонаправленные векторы – это векторы, которые имеют одинаковое направление. Они указывают в одну и ту же сторону, образуя угол между собой равный нулю градусов. В геометрии сонаправленные векторы являются особой категорией и часто используются для решения различных задач.
Сонаправленные векторы могут быть представлены числами или геометрическими объектами. Они играют важную роль в алгебре векторов и находят применение в физике, механике, инженерии и других науках.
Простейший пример сонаправленных векторов – векторы, указывающие вдоль одной и той же прямой линии. Например, если вектор A=[2, 0] указывает вправо по оси X, а вектор B=[-4, 0] указывает влево по оси X, то они являются сонаправленными. Оба вектора имеют одинаковое направление, в данном случае горизонтальное, и оба указывают в разные стороны.
Сонаправленные векторы также могут иметь разную длину. Векторы A=[3, 0] и B=[6, 0] также являются сонаправленными, но вектор B имеет двукратно большую длину по сравнению с вектором A. Тем не менее, они все равно указывают в одну и ту же сторону и образуют угол равный нулю градусов.
Сонаправленные вектора в геометрии: определение и примеры

Одним из способов определить, являются ли два вектора сонаправленными, является проверка, есть ли у них одинаковое направление. Для этого можно использовать равенство направляющих векторов - если координаты направляющих векторов двух векторов совпадают, то эти векторы сонаправленны.
Примеры сонаправленных векторов в геометрии:
- Векторы, направленные вдоль одной прямой: Например, векторы, указывающие на одну и ту же точку на числовой оси. Вектор с направлением "вправо" и вектор с направлением "влево" на числовой оси - это примеры сонаправленных векторов.
- Векторы, направленные вдоль одного направления: Например, векторы, указывающие на одну и ту же точку в пространстве. Если два вектора указывают вверх, то они сонаправлены. Если они указывают вниз - они тоже сонаправлены, но в противоположном направлении.
Сонаправленные векторы имеют важное значение в геометрии, так как они позволяют нам понять, находятся ли два вектора в одном направлении или же находятся ли они в противоположных направлениях. Это важно при решении различных задач и определении свойств геометрических объектов.
Что такое сонаправленные вектора?
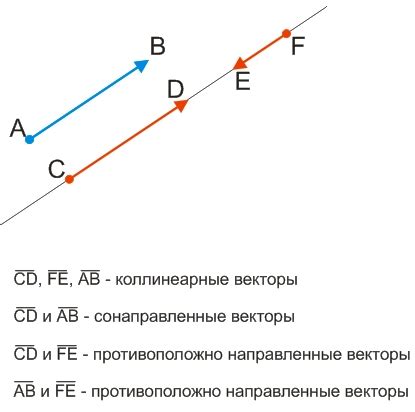
Для двух векторов, чтобы они были сонаправленными, их направления должны совпадать или быть противоположными, их длины могут быть различными. Сонаправленные векторы могут быть положительными или отрицательными, в зависимости от их ориентации.
Сонаправленные векторы встречаются во многих задачах геометрии. Например, вектор скорости и вектор ускорения движения объекта могут быть сонаправленными, если объект движется в одном направлении с постоянным ускорением.
Если вектор сонаправлен с самим собой, то он называется коллинеарным. Коллинеарные векторы - это частный случай сонаправленных векторов, когда они имеют одинаковое направление и неравные длины.
Основные свойства сонаправленных векторов

Сонаправленные векторы в геометрии обладают несколькими ключевыми свойствами:
- Сонаправленные векторы имеют одинаковое направление и ориентацию: Если два вектора сонаправлены, то они указывают в одном и том же направлении и имеют одинаковую ориентацию. Например, вектор A и вектор B являются сонаправленными, если они указывают в одном и том же направлении, например, вправо.
- Сонаправленные векторы могут быть пропорциональны: Если два вектора сонаправлены, то они могут быть выражены друг через друга с помощью постоянного множителя. Например, если вектор A равен (2, 4) и вектор B равен (4, 8), то вектор B можно выразить через вектор A с помощью множителя 2: B = 2A.
- Сонаправленные нулевые векторы: Нулевой вектор (0, 0) также считается сонаправленным с любым другим вектором. Нулевой вектор не имеет фиксированного направления или ориентации, но он сонаправлен со всеми другими векторами.
- Сумма сонаправленных векторов: Если два или более вектора сонаправлены, то их сумма будет также сонаправлена. Например, если вектор A и вектор B сонаправлены, то их сумма A + B будет также сонаправлена с ними.
Эти свойства являются фундаментальными для понимания сонаправленных векторов в геометрии и используются при решении задач, связанных с направлениями и ориентациями векторов.
Примеры сонаправленных векторов в геометрии
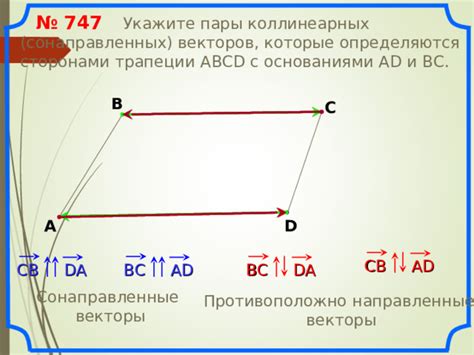
- Векторы движения автомобиля по прямой дороге. Векторы скорости исходят от начальной точки и направлены в сторону движения.
- Векторы силы, действующие на груз, поднятый по вертикальной оси. Все векторы направлены вверх или вниз в зависимости от направления силы.
- Векторы внешнего давления на поверхность жидкости в емкости. Все векторы направлены перпендикулярно к поверхности.
- Векторы электрического поля от положительного заряда. Векторы ведут себя как "лучи", выходящие из заряда и расходящиеся в пространстве.
- Векторы силы тяжести на тела, падающие свободно на Землю. Все векторы направлены вниз в сторону центра Земли.
Это лишь некоторые примеры, и в реальном мире существует множество других случаев, когда векторы могут быть сонаправленными. Знание и понимание сонаправленных векторов поможет вам анализировать и решать геометрические задачи.
Полезность сонаправленных векторов в геометрии

Сонаправленные векторы играют важную роль в геометрии и имеют множество полезных свойств и применений. Они позволяют нам понять и описать различные аспекты пространственного расположения объектов и их взаимодействия.
Одно из применений сонаправленных векторов - определение линейной независимости объектов в пространстве. Если два или более векторов сонаправлены, они лежат на одной прямой и являются линейно зависимыми. Это означает, что один вектор может быть выражен в виде линейной комбинации других векторов. Такая информация может быть полезна, например, при решении систем линейных уравнений или определении базиса пространства.
Кроме того, сонаправленные векторы помогают понять направление и ориентацию объектов в пространстве. Их направление может быть определено с помощью угла, который они образуют с некоторой фиксированной осью или плоскостью. Это позволяет нам классифицировать объекты на основе их ориентации, например, взаимное положение прямых или плоскостей в трехмерном пространстве.
Еще одним применением сонаправленных векторов является определение коллинеарности объектов. Если два или более вектора сонаправлены, они являются коллинеарными, что означает, что они лежат на одной прямой или в одной плоскости. Это позволяет нам устанавливать связи между различными объектами и анализировать их взаимное расположение и свойства.
Таким образом, сонаправленные векторы в геометрии имеют множество полезных применений. Они помогают нам анализировать и понимать различные аспекты пространственного расположения объектов, их линейную зависимость, направление, ориентацию и коллинеарность. Это позволяет нам решать различные задачи и применять геометрические концепции в реальных ситуациях.
В геометрии сонаправленные векторы могут использоваться для определения направления движения объектов, расчета сил и скоростей, а также для строительства графиков и анализа векторных полей.
Одним из примеров сонаправленных векторов является вектор скорости движения автомобиля. Если автомобиль движется прямо вперед, то его вектор скорости будет сонаправлен с направлением движения.
Сонаправленные векторы также могут использоваться для определения относительного расположения объектов. Например, если две линии параллельны, то их нормальные векторы будут сонаправлены, т.е. будут иметь одинаковое направление.
Из вышесказанного следует, что сонаправленные векторы имеют важное значение в геометрии и находят широкое применение. Они позволяют нам анализировать и понимать различные геометрические свойства и отношения в пространстве.



