Серединный перпендикуляр – это перпендикуляр, опущенный из центра отрезка к середине этого отрезка. Он является одной из основных геометрических конструкций и обладает рядом важных свойств.
Прежде всего, стоит отметить, что серединный перпендикуляр всегда проходит через середину отрезка и делит его на две равные части. Это свойство позволяет использовать его для построения равнобедренных и равносторонних треугольников, а также для вычисления площади фигур.
Кроме того, серединный перпендикуляр является осью симметрии для отрезка. Это означает, что если точку находится на этой оси, то ее отражение симметрично расположено относительно серединного перпендикуляра. Это свойство облегчает решение различных геометрических задач, например, построение симметричных фигур или определение точек, симметричных относительно заданной точки.
Серединный перпендикуляр: определение, свойства, применение

Основные свойства серединного перпендикуляра:
- Серединный перпендикуляр равноудален от концов отрезка.
- Серединный перпендикуляр делит отрезок пополам.
- Серединный перпендикуляр является осью симметрии для отрезка.
Серединный перпендикуляр имеет важное практическое применение:
- В геометрии, серединный перпендикуляр используется для нахождения середины отрезка без его измерения.
- В архитектуре и инженерии, серединный перпендикуляр применяется для построения перпендикулярных линий и нахождения центральных точек.
- В кристаллографии, серединный перпендикуляр используется для определения симметрии кристаллов.
Определение серединного перпендикуляра
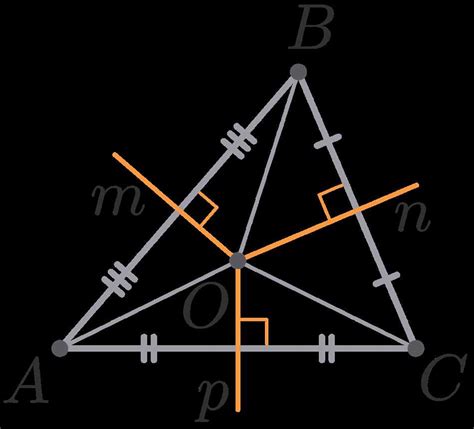
Для построения серединного перпендикуляра необходимо найти середину заданного отрезка. Затем, проведя перпендикулярную прямую через эту точку, получим серединный перпендикуляр.
Свойства серединного перпендикуляра:
- Серединный перпендикуляр делит исходный отрезок на две равные части.
- Серединный перпендикуляр является осью симметрии для исходного отрезка.
- Серединный перпендикуляр касается окружности, описанной вокруг исходного отрезка, в его середине.
- Серединный перпендикуляр двух пересекающихся отрезков является их общим перпендикуляром.
Свойства серединного перпендикуляра
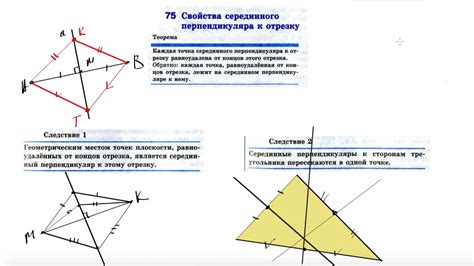
У серединного перпендикуляра есть несколько важных свойств:
| Свойство | Описание |
| 1 | Серединный перпендикуляр равноудален от концов отрезка. |
| 2 | Серединный перпендикуляр делит отрезок на две равные части. |
| 3 | Серединный перпендикуляр одновременно является биссектрисой угла, образованного отрезком и его продолжением. |
Используя эти свойства, серединный перпендикуляр может использоваться для нахождения середины отрезка, определения равенства отрезков и нахождения точки пересечения прямых.
Геометрическое свойство серединного перпендикуляра
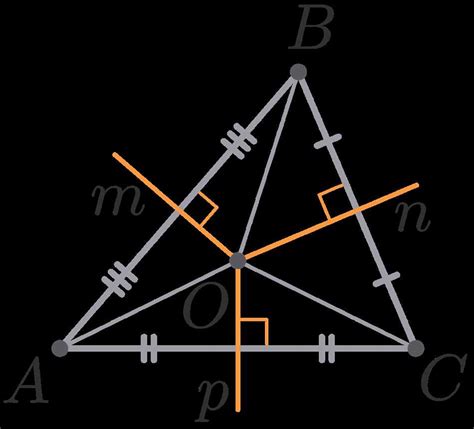
Геометрическое свойство серединного перпендикуляра заключается в том, что он делит отрезок пополам, то есть создает два равных отрезка. Другими словами, серединный перпендикуляр является линией, которая соединяет середину отрезка с его концами и делит его на две равные части.
Это свойство можно использовать для нахождения середины отрезка, если известны его концы. Для этого нужно провести серединный перпендикуляр к данному отрезку. Точка пересечения этого перпендикуляра и самого отрезка будет являться серединой отрезка, поскольку перпендикуляр делит отрезок пополам.
Геометрическое свойство серединного перпендикуляра также позволяет решать различные задачи в геометрии, связанные с равенством длин отрезков. Например, если два отрезка имеют общий серединный перпендикуляр и этот перпендикуляр делит каждый отрезок на две равные части, то эти отрезки равны по длине.
Серединный перпендикуляр треугольника

Основные свойства серединного перпендикуляра:
- Серединный перпендикуляр треугольника всегда проходит через его центр описанной окружности.
- Серединный перпендикуляр треугольника делит его на две равные части, то есть каждая из сторон треугольника делится им пополам.
- В каждом треугольнике можно провести три серединных перпендикуляра, и они все пересекаются в одной точке. Эта точка называется центром окружности, вписанной в треугольник.
- Серединный перпендикуляр треугольника является прямой симметрии треугольника, так как при отражении треугольника относительно этой прямой получается совпадающая фигура.
Серединный перпендикуляр треугольника является важным инструментом для решения геометрических задач и для изучения свойств треугольников в целом. Он помогает легко находить такие элементы треугольника, как середины сторон, центр описанной и вписанной окружности, а также является базой для построения других геометрических фигур.
Применение серединного перпендикуляра
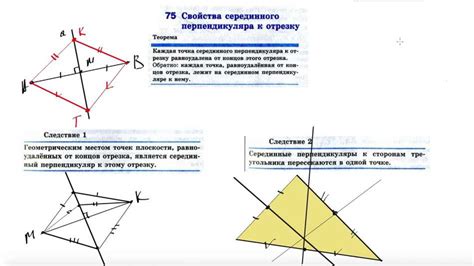
Серединный перпендикуляр имеет множество практических применений в различных областях, включая геометрию, архитектуру, конструирование и картографию. Ниже приведены некоторые из основных применений серединного перпендикуляра:
- Нахождение середины отрезка: Серединный перпендикуляр позволяет точно определить середину отрезка. Это особенно полезно при измерении расстояний и строительстве.
- Построение перпендикуляра: Серединный перпендикуляр может использоваться для построения перпендикулярной линии к заданной прямой. Это важно в архитектуре и строительстве, где точность и перпендикулярность играют важную роль.
- Нахождение центра окружности: Если известны две точки на окружности, серединный перпендикуляр к отрезку, соединяющему эти точки, проходит через центр окружности. Это свойство помогает в геометрии и конструировании.
- Картография: Серединные перпендикуляры играют важную роль в создании карт и определении масштаба. Они позволяют ровно разделить карту на равные части и достичь точности при представлении пространства на плоскости.
- Криптография: Серединный перпендикуляр может применяться в криптографии для построения и анализа шифров. Он может использоваться для нахождения ключевых значений и разделения информации на равные части.
Это лишь некоторые из множества применений серединного перпендикуляра. Важно помнить, что его свойства и возможности могут быть использованы в различных контекстах в зависимости от задачи.



