Развернутый угол – это особый вид угла, который имеет величину 180 градусов. Это самый большой угол, который можно представить, так как он соединяет противоположные направления на плоскости.
Развернутый угол можно представить как полукруг, где концы полуокружности образуют две прямые линии, называемые сторонами угла. Обычно развернутый угол обозначается символом "∟".
Этот вид угла не только широко применяется в математике, но и является важным понятием в геометрии, физике и других науках. Например, в геометрии он часто используется при изучении треугольников, параллельных и перпендикулярных линий, а также при измерении поворотов и поворачиваний в пространстве.
Однако важно отметить, что в контексте геометрии и математики "развернутый угол" имеет строгое определение и отличается от других типов углов, таких как прямой угол или тупой угол. Развернутый угол всегда является половиной полного оборота и может быть полезным инструментом для анализа и решения математических задач.
Значение и свойства углов в геометрии
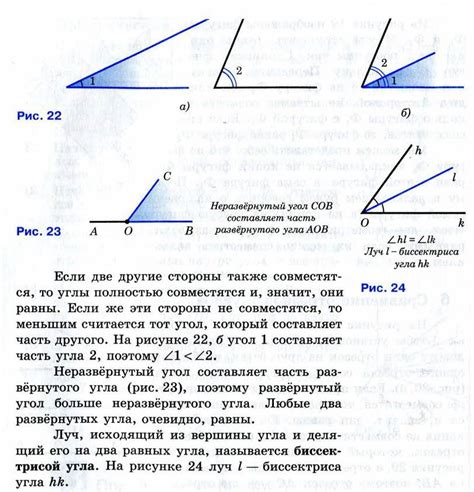
В геометрии углом называется фигура, образованная двумя лучами, которые имеют общий начальный пункт. Углы широко используются в математике и имеют свои особенности и свойства.
Значение угла измеряется в градусах. Полный угол равен 360°, а угол, который занимает половину полного угла, называется прямым углом и равен 90°. Важно знать, что сумма всех углов внутри треугольника равна 180°, а в прямоугольнике 360°.
Углы могут быть разных типов. Например, острые углы имеют меньше 90°, тупые углы больше 90°, а прямые углы равны 90°. Также существуют равные углы, которые имеют одинаковую величину, и вертикальные углы, которые образуются пересекающимися прямыми. Вертикальные углы равны.
Для измерения углов можно использовать геометрические инструменты, такие как угломер или транспортир. Также существуют методы расчета углов с помощью синусов, косинусов и тангенсов.
Понимание значения и свойств углов в геометрии является важной основой для решения задач и анализа геометрических фигур. Знание этих свойств позволяет определить геометрические формы и вычислить их параметры.
Геометрические фигуры и углы
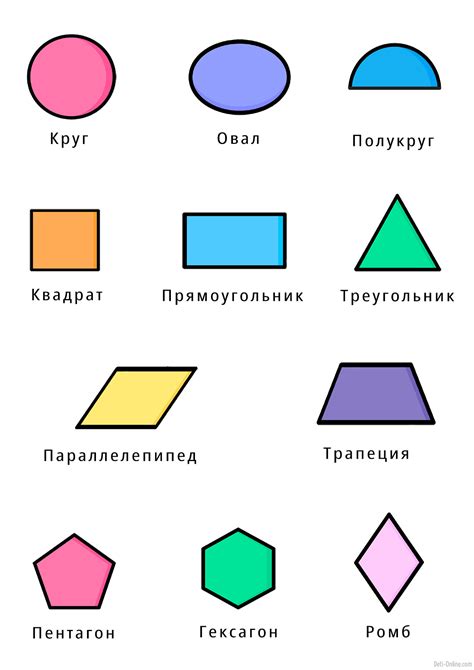
Угол - это фигура, образованная двумя лучами, которые исходят из одной точки, называемой вершиной угла. Углы могут быть различной величины и формы, и они имеют важное значение в различных областях математики и науки.
Развернутый угол - это особый вид угла, который равен 180 градусам, или π радианам. Визуально развернутый угол представляет собой прямую линию.
Важно отметить, что развернутый угол обладает рядом свойств:
- Он является большим углом, так как он перекрывает полную полуплоскость.
- Он является конгруэнтным своей противоположной части. Если развернутый угол повернуть на 180 градусов, получится прямой угол.
- Он разделяет плоскость на две равные полуплоскости.
Развернутый угол имеет ряд приложений, включая измерение и построение углов, а также в решении геометрических задач и проблем.
Углы в плоских фигурах
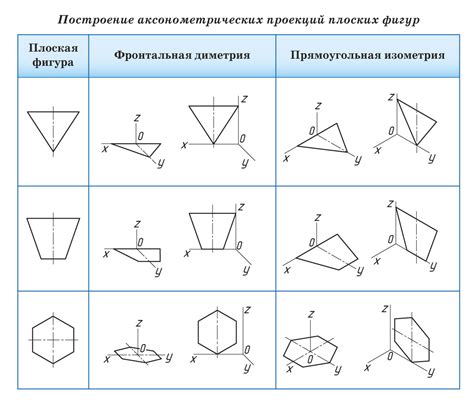
В плоских фигурах, таких как треугольники, прямоугольники или параллелограммы, углы играют важную роль. Они определяют форму и свойства фигуры, помогая в классификации и изучении ее свойств.
В зависимости от величины угла, его можно классифицировать как развёрнутый (более 180 градусов), прямой (равный 90 градусам), острый (меньше 90 градусов) или тупой (больше 90 градусов).
Примеры:
Угол, равный 90 градусам, называется прямым углом. Это угол, который образуется двумя перпендикулярными линиями.
Угол, меньший 90 градусов, называется острым углом. Например, в прямоугольнике каждый угол равен 90 градусам, поэтому все его углы являются острыми углами.
Угол, больший 90 градусов, называется тупым углом. Например, в треугольнике, если один угол больше 90 градусов, то он является тупым углом.
Знание о свойствах углов в плоских фигурах помогает в решении задач на доказательство геометрических фактов, нахождение неизвестных углов и многое другое.
Углы и их свойства в пространстве
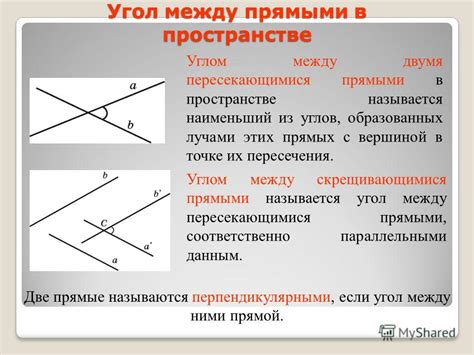
В математике углом называется геометрическая фигура, состоящая из двух лучей с общей начальной точкой, называемой вершиной угла. Угол обозначается символом α.
В пространстве существуют различные виды углов, которые обладают своими особенностями и свойствами. Некоторые из них включают:
- Прямой угол: это угол, который равен 90 градусам. Он обозначается символом α = 90°. Прямой угол делит плоскость на две перпендикулярные линии.
- Острый угол: это угол, который меньше 90 градусов. Острый угол обозначается символом α < 90°. Он характеризуется тем, что его стороны расположены внутри полуокружности.
- Тупой угол: это угол, который больше 90 градусов. Тупой угол обозначается символом α > 90°. Здесь стороны угла располагаются за пределами полуокружности.
- Выпуклый угол: это угол, у которого все точки лежат внутри или на границе сферы, так что сумма всех его углов равна 360 градусам.
- Вогнутый угол: это угол, который имеет как минимум одну сторону внутри сферы.
Углы в пространстве играют ключевую роль в геометрии и используются для измерения и моделирования различных физических явлений. Понимание свойств и типов углов является важным для решения задач и построения точных математических моделей.
Развернутый угол и его характеристики
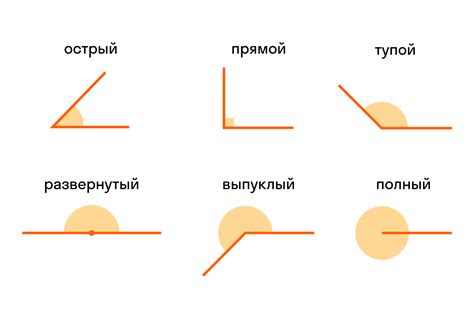
Основные характеристики развернутого угла:
1. Мера: развернутый угол всегда имеет меру 180 градусов. Это означает, что он представляет полную окружность и занимает все доступное пространство вокруг точки.
2. Расположение: развернутый угол может быть расположен в любой части плоскости. Он может быть полностью расположен внутри фигуры, пересекать ее или быть полностью за ее пределами.
3. Соседство: развернутые углы всегда имеют смежные углы. Это означает, что одна из сторон развернутого угла - это также сторона другого угла. Смежные углы могут быть полностью совпадающими или иметь общую сторону.
4. Сумма: развернутые углы, вместе с другими углами, образуют полную окружность с суммой 360 градусов. Таким образом, два развернутых угла образуют вместе плоский угол со суммой 360 градусов.
Развернутый угол играет важную роль в геометрии и широко применяется в различных областях, таких как инженерия, архитектура и физика.
Углы и их измерение
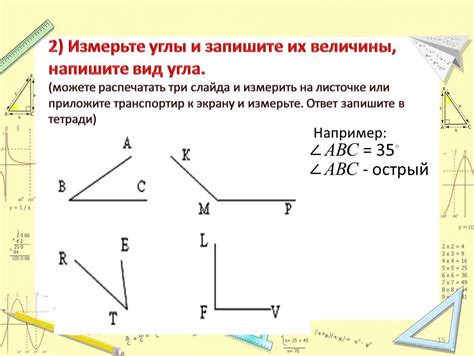
Углы могут быть разных типов, в зависимости от их внешнего вида. Один из таких типов - развернутый угол. Развернутый угол - это угол, который равен 180 градусам или пи радианам. Он обозначается символом ∡.
Мера угла определяется с помощью градусной меры или радианной меры. Градусная мера основана на делении окружности на 360 равных частей, где каждая часть равна 1 градусу. Радианная мера основана на длине дуги окружности и равна отношению длины дуги к радиусу окружности.
Развернутый угол имеет наибольшую меру среди всех типов углов. Он представляет собой полный поворот вокруг вершины угла и эквивалентен двум прямым углам.
Знание о развернутых углах полезно при решении задач геометрии и позволяет лучше понять структуру углов и их свойства.
Развернутый угол в математике 5 класса
Угол можно представить как две лучи, выходящие из одной точки, которые могут развернуться по разные стороны. Если угол развернут на 180 градусов, то лучи продолжатся в противоположных направлениях.
Развернутый угол может быть встречен в различных геометрических задачах. Например, в задачах о построении фигур или при работе с поворотами и симметрией.
Для работы с развернутыми углами в 5 классе дети изучают основные понятия геометрии и учатся образовывать и измерять углы с помощью транспортира.
Пример:
Дан угол САВ, в котором угол САВ равен 180 градусов. Угол САВ – это развернутый угол, так как его значение составляет половину оборота.
Развернутый угол является важным понятием в геометрии 5 класса, и его изучение поможет учащимся понять основные принципы построения и измерения углов.
Примеры задач и упражнений на развернутые углы

Задача 1:
Найдите развернутый угол, если известно, что его смежные углы равны 55° и 125°.
Решение: Угол равен сумме смежных углов. Поэтому развернутый угол равен 55° + 125° = 180°.
Задача 2:
Определите меру развернутого угла, если его внутренний угол составляет 100°.
Решение: Мера развернутого угла равна 180° минус мера внутреннего угла. Поэтому развернутый угол равен 180° - 100° = 80°.
Задача 3:
Найдите меру внутреннего угла развернутого угла, если его смежный угол составляет 120°.
Решение: Мера внутреннего угла развернутого угла равна 180° минус мера смежного угла. Поэтому внутренний угол развернутого угла равен 180° - 120° = 60°.
Упражнение 1:
Найдите меру развернутого угла, если два его смежных угла равны 80° и 100°.
Решение: Угол равен сумме смежных углов. Поэтому развернутый угол равен 80° + 100° = 180°.
Упражнение 2:
Найдите меру внутреннего угла развернутого угла, если его смежный угол составляет 150°.
Решение: Мера внутреннего угла развернутого угла равна 180° минус мера смежного угла. Поэтому внутренний угол развернутого угла равен 180° - 150° = 30°.
Упражнение 3:
Определите меру развернутого угла, если его внутренний угол равен 120°.
Решение: Мера развернутого угла равна 180° минус мера внутреннего угла. Поэтому развернутый угол равен 180° - 120° = 60°.



