Рациональные числа являются одной из основных групп чисел в математике. Рациональные числа могут быть представлены в виде дробей, где числитель и знаменатель являются целыми числами, а знаменатель не равен нулю.
Рациональные числа включают в себя как положительные, так и отрицательные числа. Например, -3, 2 и 5/7 - все они являются рациональными числами.
Определение рациональных чисел можно сформулировать следующим образом: рациональные числа - это все числа, которые можно представить в виде дроби, где числитель и знаменатель являются целыми числами.
Примерами рациональных чисел могут служить обыкновенные дроби, такие как 1/2, 3/4 и 5/6. Десятичные числа, которые также повторяются, такие как 0.3333..., также являются рациональными числами.
Определение рациональных чисел
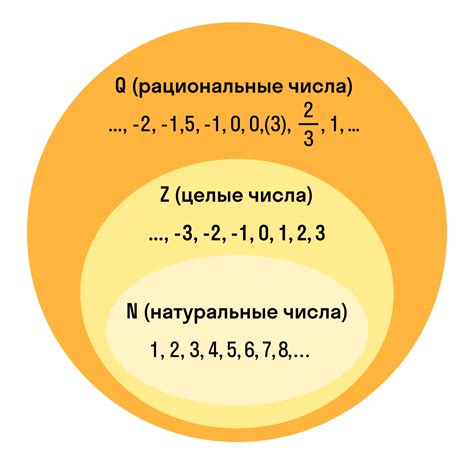
Рациональные числа включают в себя целые числа (например, 0, 1, -5) и десятичные дроби (например, 0,25, -0,75, 2,33333). Десятичные дроби могут быть как конечными, так и периодическими: например, 0,33333 или 0,142857142857.
Рациональные числа можно складывать, вычитать, умножать и делить друг на друга. Операции с рациональными числами также могут включать приведение дробей к общему знаменателю, сокращение дробей и расширение десятичных дробей путем добавления нулей после десятичной запятой.
Рациональные числа играют важную роль в математике и ежедневной жизни. Они используются для измерения и подсчета, а также в финансах и науке. Также они являются основой для дальнейших изучений, включая иррациональные числа и вещественные числа.
Рациональные числа: что это такое? Определение и свойства
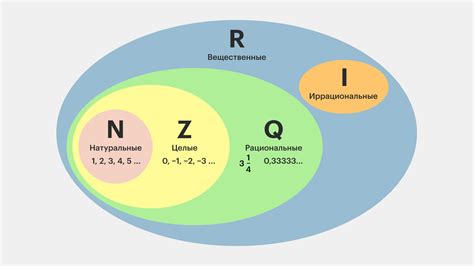
Рациональные числа включают в себя все целые числа, так как любое целое число может быть представлено как дробь с знаменателем, равным 1. Кроме того, рациональные числа включают в себя все обыкновенные десятичные дроби: конечные, периодические и бесконечные.
Основное свойство рациональных чисел заключается в том, что они образуют поле – математическую структуру, где определены операции сложения, вычитания, умножения и деления. Для рациональных чисел выполняются коммутативные, ассоциативные и дистрибутивные свойства этих операций.
Кроме того, рациональные числа обладают еще рядом интересных свойств, таких как:
- Плотность – между любыми двумя рациональными числами существует бесконечное количество других рациональных чисел;
- Плотность относительно иррациональных чисел – между любыми двумя рациональными числами существует бесконечное количество иррациональных чисел;
- Бесконечность множества рациональных чисел – множество рациональных чисел счетно бесконечно, то есть его элементы можно упорядочить в последовательность, пронумеровав их натуральными числами.
Рациональные числа являются важным понятием в математике и находят широкое применение в решении задач как теоретического, так и практического характера. Изучение рациональных чисел помогает лучше понять и описать мир вокруг нас, позволяя решать сложные математические задачи, а также применять эти знания в других областях науки и техники.



