Прямая и обратная пропорциональность - это понятия, широко используемые в математике и физике для описания соотношения между двумя переменными. Они помогают нам понять, как изменения в одной переменной влияют на другую.
Прямая пропорциональность возникает, когда две переменные изменяются в одном направлении: если одна переменная возрастает, то и другая тоже возрастает, и наоборот. Это означает, что соотношение между переменными остается постоянным. Например, если увеличить количество работы, то и время, затрачиваемое на нее, увеличится пропорционально. Часто этот тип пропорциональности обозначают как "y пропорционально x".
С другой стороны, обратная пропорциональность возникает, когда две переменные изменяются в противоположных направлениях: если одна переменная увеличивается, то другая уменьшается, и наоборот. Это означает, что произведение двух переменных остается постоянным. Например, если увеличить скорость движения, то время, затрачиваемое на преодоление расстояния, уменьшится обратно пропорционально. Часто этот тип пропорциональности обозначают как "y обратно пропорционально x".
Знание о прямой и обратной пропорциональности позволяет нам более точно анализировать и планировать различные ситуации. Эти концепции находят применение во многих областях, таких как экономика, бизнес, физика, биология и многие другие. Понимая эти принципы, мы можем предсказать результаты изменений величин и принимать решения, основанные на этом знании.
Прямая и обратная пропорциональность: суть и принципы
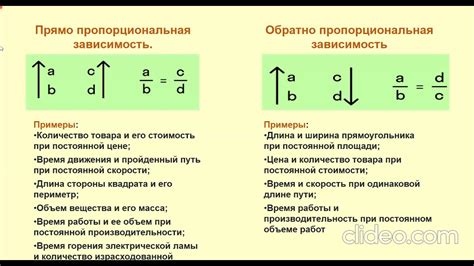
Прямая пропорциональность означает, что две величины изменяются одновременно в одном направлении: если одна величина увеличивается, то другая также увеличивается, и наоборот. Например, количество времени, затрачиваемое на выполнение задачи, и количество задач, выполненных за этот период, могут быть в прямой пропорции.
Обратная пропорциональность, наоборот, означает, что две величины изменяются в противоположных направлениях: если одна величина увеличивается, то другая уменьшается, и наоборот. Например, время, затрачиваемое на выполнение задачи, и скорость выполнения задач могут быть в обратной пропорции.
Для понимания пропорциональности необходимо использовать принципы, основанные на математических алгоритмах. Для прямой пропорциональности используется формула: x/y = k, где x и y - две величины, k - постоянный коэффициент пропорциональности.
Для обратной пропорциональности также используется формула: xy = k. В данном случае k также является постоянным коэффициентом пропорциональности, однако знак умножения указывает на противоположность изменения величин.
Прямая и обратная пропорциональность представляют собой важные инструменты для анализа данных и решения различных задач. Понимание и применение этих концепций помогает исследователям и практикам эффективно использовать данные и прогнозировать результаты.
Определение прямой пропорциональности

Формально, две переменные x и y, являются прямо пропорциональными, если отношение между ними постоянно. Это можно записать следующим образом:
y = kx
где y – зависимая переменная, x – независимая переменная, k – постоянная прямой пропорциональности.
Если мы зададим какое-то значение x, то можем вычислить соответствующее значение y, применив формулу выше. Аналогично, зная y, можно найти x.
Прямая пропорциональность характеризуется тем, что график зависимости переменной y от x будет представлять собой прямую линию, проходящую через начало координат.
| x | y |
|---|---|
| 1 | k |
| 2 | 2k |
| 3 | 3k |
| 4 | 4k |
| 5 | 5k |
В таблице выше представлены значения переменных x и y для прямой пропорциональности. Заметим, что при увеличении значения x, значение y также увеличивается в том же пропорциональном соотношении с коэффициентом прямой пропорциональности k.
Определение обратной пропорциональности

В обратной пропорциональности, когда одна переменная увеличивается, другая переменная уменьшается и наоборот. Отношение между этими переменными можно записать в виде:
если x и y - две переменные, то обратная пропорциональность может быть представлена следующим образом:
y = k/x, где k - постоянная пропорциональности.
Здесь константа k определяет силу обратной пропорциональности и может принимать любое положительное значение.
Примером обратной пропорциональности может быть зависимость между скоростью движения и временем, затраченным на преодоление заданного расстояния. Чем больше скорость, тем меньше времени потребуется для преодоления расстояния, и наоборот.
Обратная пропорциональность является важным концептом в математике и широко применяется в физике, экономике, статистике и других науках для описания функциональных связей между переменными.
Принципы прямой пропорциональности

Существует несколько принципов, которые определяют прямую пропорциональность:
- Принцип постоянного отношения. В прямой пропорции отношение между двумя величинами всегда остается постоянным.
- Принцип независимости. Величины, находящиеся в прямой пропорциональности, не зависят друг от друга, то есть изменение одной величины не влияет на изменение другой.
- Принцип возрастания. При прямой пропорции увеличение одной величины приводит к увеличению другой, а уменьшение одной величины – к уменьшению другой.
- Принцип нулевой точки. При прямой пропорциональности значение одной из величин не равно нулю.
Принципы прямой пропорциональности применяются в различных областях науки и повседневной жизни, например, в физике, экономике, математике и т.д. Они позволяют анализировать и предсказывать изменение одной величины при изменении другой. Важно уметь распознавать и применять принципы прямой пропорциональности для решения задач и построения связей между величинами.
Принципы обратной пропорциональности

Пропорциональность двух величин называется обратной, если при увеличении одной из них, другая уменьшается, и наоборот. В обратной пропорциональности меняется отношение между величинами: при увеличении одной величины, другая уменьшается с увеличением в несколько раз. При этом произведение обратно пропорциональных величин всегда остается постоянным.
Принципы обратной пропорциональности можно выразить следующим образом:
| 1. | Чем больше значение одной величины, тем меньше значение другой величины. |
| 2. | Чем меньше значение одной величины, тем больше значение другой величины. |
| 3. | При умножении или делении одной величины на число, другая величина умножается или делится на это число. |
| 4. | Произведение обратно пропорциональных величин всегда остается постоянным. |
Обратная пропорциональность широко применяется в различных областях, таких как физика, химия, экономика и т.д. Например, закон Ома в электрической цепи является примером обратной пропорциональности: с увеличением сопротивления снижается сила тока.



