Возможно, вы уже слышали о понятии "произвольная прямая" в математике. Но что это на самом деле означает? Давайте разберемся.
Произвольная прямая - это прямая, которая может быть нарисована в произвольном положении на плоскости. Она не имеет никаких ограничений и может быть направлена в любом направлении. Важно понимать, что произвольная прямая не всегда проходит через начало координат или имеет какие-либо другие особенности.
Когда мы говорим о произвольной прямой, мы обычно используем букву "l" для ее обозначения. Например, "l" может означать произвольную прямую, а "AB" - отрезок или линию, принадлежащую этой произвольной прямой.
Произвольные прямые широко используются в геометрии, чтобы изучать свойства и взаимодействия различных фигур. Знание о произвольной прямой поможет вам лучше понять, как работает геометрия и решать математические задачи связанные с фигурами и их свойствами.
Данное представление "Произвольная прямая в математике"
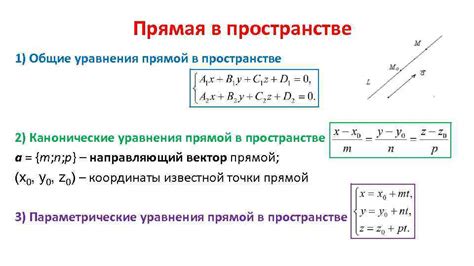
Произвольная прямая в математике представляет собой линию, которая не имеет фиксированного положения или направления. Это означает, что прямая может быть нарисована в любом месте на плоскости и может быть направлена в любом направлении.
Произвольная прямая является основным понятием в геометрии и используется для определения и изучения других фигур и объектов. Например, линейные углы могут быть измерены с помощью произвольной прямой, а пересечение двух произвольных прямых может использоваться для определения точки пересечения.
Произвольная прямая также может быть использована для построения различных геометрических фигур, таких как треугольники, четырехугольники и многоугольники. Путем рисования или моделирования произвольной прямой и соединения ее с другими точками или объектами, можно создать различные комбинации и варианты фигур.
Понимание произвольной прямой в математике важно для развития навыков геометрического мышления и решения геометрических задач. Она также является основой для изучения других понятий, таких как отрезки и лучи, а также для понимания принципов и свойств геометрических фигур.
Определение произвольной прямой
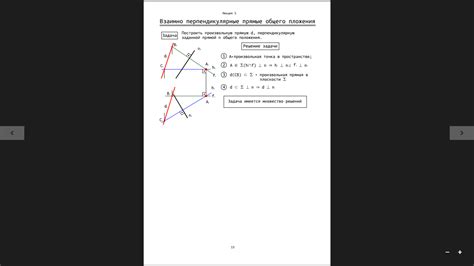
Произвольная прямая не имеет определенной длины или угла наклона. Она может быть короткой или длинной, плавной или изогнутой. Единственное требование для произвольной прямой - это то, что она должна проходить через две точки.
Произвольные прямые имеют широкое применение в математике, физике, инженерии и других науках. Они используются для моделирования и анализа различных систем и явлений. Также произвольные прямые могут быть использованы для измерения расстояний и углов, построения графиков и диаграмм, а также для создания геометрических фигур.
Свойства произвольной прямой

Свойства произвольной прямой:
- Произвольная прямая не имеет начала или конца. Она простирается бесконечно в обе стороны.
- Произвольная прямая может пересекать другие прямые, образуя точки пересечения.
- Произвольная прямая может быть параллельна другой прямой. Параллельные прямые никогда не пересекаются.
- Произвольная прямая может быть перпендикулярна другой прямой. Перпендикулярные прямые образуют прямой угол, равный 90 градусам.
- Произвольная прямая может быть наклонной, в таком случае она не является ни параллельной, ни перпендикулярной другим прямым.
Изучая свойства произвольной прямой, мы можем узнать много интересного о позиции и взаимодействии прямых на плоскости. Это поможет нам решать различные задачи и строить различные геометрические фигуры.
Использование произвольной прямой в задачах

В математике, произвольные прямые часто используются для решения различных задач. Например, мы можем использовать произвольную прямую для нахождения середины отрезка. Для этого мы проводим произвольную прямую через концы отрезка и находим точку пересечения с этой прямой – это и будет середина отрезка.
Также, произвольные прямые могут использоваться для построения треугольников. Построение треугольников с помощью произвольных прямых позволяет нам определить соотношения между сторонами и углами треугольника.
Кроме того, произвольные прямые полезны при решении задач на нахождение параллельных и перпендикулярных прямых. Мы можем использовать произвольную прямую в сочетании с другими прямыми для определения, являются ли они параллельными или перпендикулярными.
Таким образом, использование произвольной прямой в задачах позволяет нам расширить наши знания и навыки в области геометрии. Произвольные прямые помогают нам решать разнообразные задачи, а также развивают наше понимание отношений между различными геометрическими объектами.



