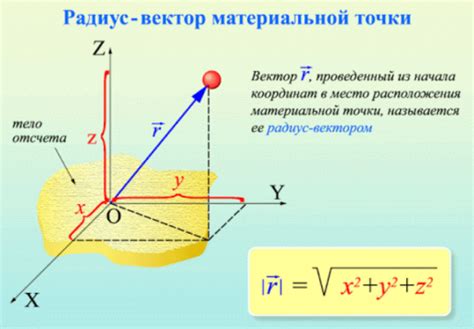
Проекции радиуса вектора – это понятие, широко используемое в математике и физике. Оно позволяет разбить радиус вектор, указывающий на точку в пространстве, на две составляющие – горизонтальную и вертикальную. Такое разложение позволяет лучше понять движение объекта, его положение и скорость.
Горизонтальная проекция радиуса вектора определяет положение объекта на плоскости или горизонтальную плоскость. Она позволяет определить расстояние объекта от начала координат до его положения на плоскости или горизонтальной плоскости. Величина горизонтальной проекции изменяется со временем, если объект перемещается.
Вертикальная проекция радиуса вектора показывает, насколько объект отклоняется от горизонтальной плоскости. Эта величина определяет высоту объекта относительно горизонтальной плоскости. Если объект движется вертикально вверх или вниз, вертикальная проекция будет изменяться.
Чтобы получить проекции радиуса вектора, необходимо использовать математические формулы и методы. Одним из способов является использование тригонометрии, а именно функций синуса и косинуса. Горизонтальная и вертикальная проекции радиуса вектора могут быть найдены с помощью соответствующих формул, описывающих связь между радиусом вектора и проекциями.
Проекции радиуса вектора: что это и как работают?
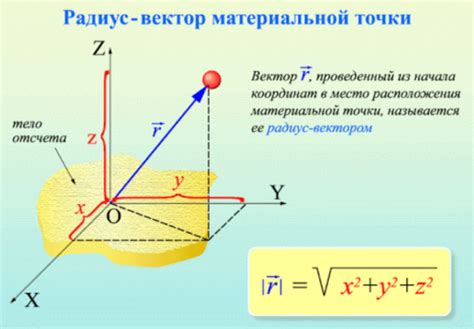
Для того чтобы вычислить проекции радиуса вектора, необходимо знать его координаты. Пусть A - это радиус вектор точки на плоскости, то есть вектор, соединяющий начало координат O с точкой A.
Проекцию радиуса вектора на ось OX можно вычислить, умножив длину вектора на косинус угла, образованного вектором с положительным направлением оси OX. Формула для вычисления проекции радиуса вектора на ось OX выглядит следующим образом:
| Проекция на ось OX: | Ax = |A| * cos(α) |
|---|
Аналогично, проекцию радиуса вектора на ось OY можно вычислить, умножив длину вектора на косинус угла, образованного вектором с положительным направлением оси OY. Формула для вычисления проекции радиуса вектора на ось OY выглядит следующим образом:
| Проекция на ось OY: | Ay = |A| * cos(β) |
|---|
Где |A| - длина радиуса вектора, α - угол между вектором и осью OX, β - угол между вектором и осью OY.
Таким образом, проекции радиуса вектора представляют собой числовые значения, которые позволяют определить длину и направление вектора по его составляющим. Это важный инструмент в физике, геометрии, программировании и других областях, где используются векторы.
Определение проекций радиуса вектора
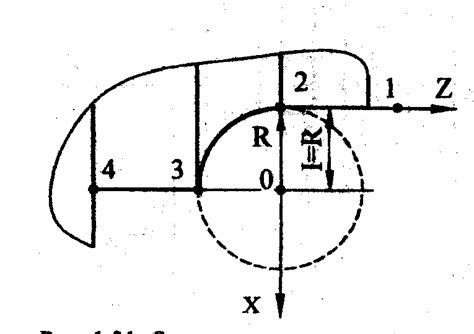
Проекция радиуса вектора на координатную ось представляет собой отрезок, образованный пересечением этой оси с прямой, проходящей через начало координат и точку, обозначающую конец радиуса вектора. Проекции радиуса вектора обычно обозначаются буквами x, y и z для осей соответственно.
Проекции радиуса вектора могут быть положительными или отрицательными в зависимости от направления вектора. Если проекция положительна, то точка находится по ту сторону оси, откуда она начинается. Если проекция отрицательна, то точка находится по противоположную сторону оси.
Проекции радиуса вектора используются во многих областях науки и техники, таких как физика, инженерия и компьютерная графика. Они позволяют вычислять координаты точек, определять расстояния и углы между векторами, а также решать различные геометрические задачи.
Использование проекций радиуса вектора в математике
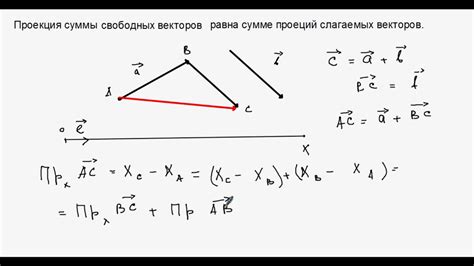
Вектор и его проекции радиуса могут использоваться для решения различных задач. Например, в геометрии проекции радиуса вектора используются для нахождения расстояния между точками, определения углов и расчета координат точек на плоскости.
Проекции радиуса вектора также находят применение в физике, где они используются для анализа движения тел и вычисления различных физических величин, таких как скорость и ускорение.
Для работы с проекциями радиуса вектора обычно используются различные методы, в том числе методы проекции на координатные оси. При этом проекция вектора на ось равна произведению длины вектора на косинус угла между вектором и данной осью.
Проекции радиуса вектора могут быть представлены таблицей, где в столбцах указываются коэффициенты относительно каждой оси. Данная таблица позволяет наглядно представить разложение вектора на проекции и производить необходимые вычисления.
| Ось | Проекция |
|---|---|
| x | rx |
| y | ry |
| z | rz |
Использование проекций радиуса вектора позволяет упростить анализ векторных пространств и сделать вычисления более удобными и понятными. Они являются неотъемлемой частью математики и находят широкое применение в различных научных и инженерных областях.
Значение проекций радиуса вектора в физике
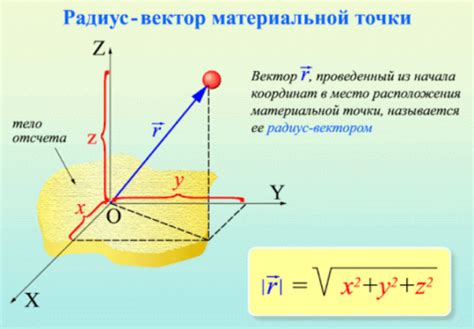
Одна из главных применений проекций радиуса вектора - анализ движения по осям. Когда объект движется вдоль одной оси, его радиус вектор может быть разложен на проекции по этой оси и осям, перпендикулярным ей. Такая декомпозиция позволяет определить скорость и ускорение объекта в разных направлениях, что имеет важное значение при решении физических задач.
Пример: Рассмотрим свободное падение тела. В этом случае радиус вектор тела будет направлен вниз, и его проекции на вертикальную ось будут отрицательными, указывая на ускорение в сторону центра Земли. При этом, проекции на горизонтальные оси будут равны нулю, так как тело движется только вдоль вертикальной оси. Это позволяет нам применять формулы и законы, специфичные для движения по одной оси, и упрощает анализ физической ситуации.
Таким образом, значение проекций радиуса вектора в физике заключается в их способности разделять движение объектов на составляющие по разным осям, что позволяет анализировать и описывать движение в пространстве. Это важное понятие используется во многих разделах физики, включая механику, динамику и гравитацию.
Применение проекций радиуса вектора в геометрии
Проекции радиуса вектора широко применяются в геометрии для решения различных задач и нахождения различных свойств объектов.
Ниже приведены некоторые примеры применения проекций радиуса вектора в геометрии:
- Определение расстояния между двумя точками: чтобы найти расстояние между двумя точками в пространстве, можно использовать проекции радиуса вектора. Найдите радиус вектор между двумя точками и вычислите его длину.
- Нахождение угла между двумя векторами: проекции радиуса вектора могут быть использованы для нахождения угла между двумя векторами. Найдите проекции радиуса вектора обоих векторов и используйте их для вычисления угла между ними.
- Поиск проекции вектора на плоскость: проекции радиуса вектора позволяют найти проекцию вектора на плоскость. Для этого найдите перпендикулярную проекцию вектора на нормаль плоскости.
- Определение компонентов вектора: проекции радиуса вектора используются для определения компонентов вектора вдоль различных осей. Найдите проекции радиуса вектора на оси координат и определите компоненты вектора.
Проекции радиуса вектора являются мощным инструментом в геометрии и позволяют решать различные задачи, связанные с векторами и пространством. Они широко используются в различных областях, таких как физика, инженерия и компьютерная графика.
Практические примеры использования проекций радиуса вектора
Проекции радиуса вектора широко применяются в сфере физики, геометрии и инженерии. Ниже приведены некоторые практические примеры использования проекций радиуса вектора:
Анализ движения тела: В механике проекция радиуса вектора используется для анализа движения тела. Проекция радиуса вектора на оси координат позволяет определить положение и перемещение тела в пространстве. Это особенно полезно при изучении траектории движения и применяется, например, при моделировании движения планет или спутников.
Разложение силы на составляющие: В физике проекции радиуса вектора используются для разложения силы на составляющие. При этом происходит разделение силы на прямую и поперечную составляющие, что позволяет более детально анализировать и понимать ее воздействие на тело. Например, при исследовании статики или динамики системы сил, разложение на составляющие помогает определить равновесие или учесть влияние трения.
Определение взаимного положения объектов: Проекции радиуса вектора используются при определении взаимного положения объектов в геометрии. Например, если нужно выяснить, пересекаются ли две фигуры или какое расстояние между ними, проекции радиуса вектора на различные оси помогают решить эти задачи. Это важно при проектировании зданий, решении геодезических задач или точного определения координат точек.
Эти лишь несколько примеров применения проекций радиуса вектора. Они демонстрируют широкий спектр использования проекций радиуса вектора в различных областях науки и инженерии.



