Призма - одно из важнейших понятий геометрии, которое изучается в 10 классе. Призма является геометрическим телом, которое имеет два полигональных основания и боковые грани, образованные параллельными линиями, соединяющими соответствующие вершины оснований.
Одно из ключевых свойств призмы - ее объем, который можно вычислить по формуле: V = S * h, где V - объем призмы, S - площадь основания, а h - высота призмы. Другими словами, чтобы найти объем призмы, нужно умножить площадь одного из оснований на высоту.
Помимо объема, призма имеет также площадь поверхности, которая вычисляется по формуле: Sп = 2Sосн + Ph, где Sп - площадь поверхности призмы, Sосн - площадь одного из оснований, P - периметр основания, а h - высота призмы.
Определение призмы в геометрии
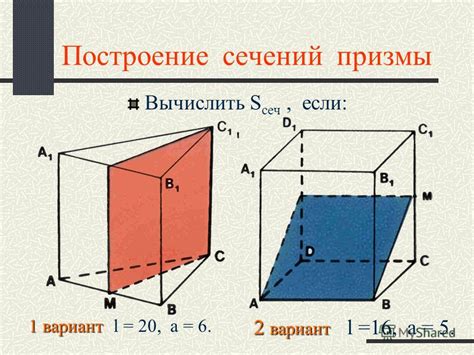
Призма может быть различных форм и размеров, в зависимости от формы оснований и количества боковых ребер. Например, если основаниями призмы являются равнобедренные треугольники, то такая призма называется треугольной призмой. Если основаниями призмы являются равные равнобедренные многоугольники с большим количеством сторон, то такая призма будет называться многоугольной призмой.
Призмы широко применяются в геометрии и имеют много полезных свойств. Например, площадь боковой поверхности призмы можно вычислить с помощью формулы, которая зависит от величины основания и высоты призмы. Также, объем призмы можно вычислить по формуле, зависящей от площади основания и высоты призмы.
Структура призмы
Каждая призма имеет два основания, которые являются равными и параллельными. Поэтому призмы можно классифицировать в зависимости от формы оснований. Например, призмы могут быть треугольными, четырехугольными, пятиугольными и т.д., и их основания могут быть правильными (все стороны и углы равны) или неправильными.
Количество боковых граней призмы определяется количеством сторон основания. Например, у треугольной призмы будет три боковые грани, у четырехугольной – четыре и т.д. Боковые ребра призмы параллельны и равны по длине.
Таким образом, структура призмы состоит из вершин, оснований, боковых граней и боковых ребер. Все эти элементы совместно образуют форму призмы и определяют ее свойства и характеристики.
Основные характеристики призмы

1. Количество граней: Призма имеет два многоугольных основания и боковые грани, соединяющие их. Общее количество граней призмы равно сумме количества граней основания и количества боковых граней.
2. Количество вершин: У призмы количество вершин равно сумме количества вершин на каждом основании и количества вершин на боковых гранях.
3. Количество ребер: Ребра призмы – это отрезки, соединяющие вершины. Их количество равно сумме количества ребер на основаниях и количества ребер на боковых гранях.
4. Форма оснований: От формы оснований призмы зависит его название. Например, если основаниями являются шестиугольники, то призма будет называться шестиугольной призмой.
5. Высота призмы: Высота призмы – это расстояние между параллельными основаниями. Она перпендикулярна плоскости основания и определяет размер призмы.
| Характеристика | Определение |
|---|---|
| Количество граней | Сумма граней основания и боковых граней |
| Количество вершин | Сумма вершин на основаниях и боковых гранях |
| Количество ребер | Сумма ребер на основаниях и боковых гранях |
| Форма оснований | Определяет название призмы |
| Высота призмы | Расстояние между основаниями призмы |
Типы призм
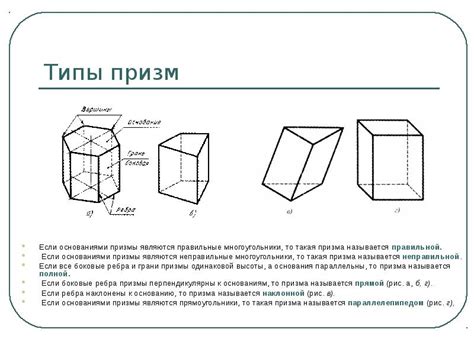
В геометрии существует несколько типов призм, которые отличаются по форме своей основы:
| Тип | Описание |
|---|---|
| Прямоугольная призма | Основой является прямоугольник. |
| Треугольная призма | Основой является треугольник. |
| Правильная призма | Все боковые грани правильного многоугольника. |
| Неправильная призма | Основная грань является неправильным многоугольником. |
Кроме того, призмы могут быть и усеченными, когда верхняя и нижняя грани имеют меньшую площадь, чем боковые грани.
Свойства призм
Свойства призм:
| 1. Площадь боковой поверхности | Площадь боковой поверхности призмы можно найти, умножив периметр основания на высоту призмы. |
| 2. Объем | Объем призмы можно найти, умножив площадь основания на высоту призмы. |
| 3. Диагональ | Диагональ призмы - это отрезок, соединяющий две вершины основания, не лежащие на одной из боковых ребер. |
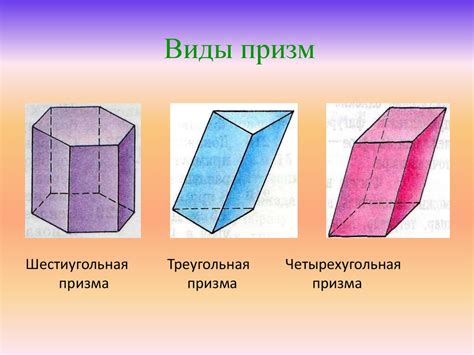
| 4. Виды призм | Существуют различные виды призм, такие как прямая призма, правильная призма, треугольная призма и многие другие. |
| 5. Другие свойства | К другим свойствам призм относятся равенство углов и сторон боковых граней, равенство диагоналей оснований и другие геометрические свойства. |
Изучение свойств призм поможет понять и применять геометрические законы и теоремы в решении задач и конструкциях в геометрии.
Примеры использования призм
Оптика: Призмы используются в оптике, чтобы изменять направление и распространение света. Одно из самых распространенных применений призм в оптике - разложение белого света на составляющие его цвета. Также призмы применяются в оптических системах, таких как бинокли, телескопы и микроскопы.
Гравюра: В гравюре призмы используются для переноса изображений на поверхности. Они способны изменять направление света, позволяя художникам создавать потрясающие яркие эффекты и линии на поверхностях различных материалов.
Строительство: Призмы применяются в строительстве для измерения и контроля углов. Они позволяют инженерам и архитекторам создавать точные геометрические формы и расчеты при планировании и построении сооружений.
Декорирование: Призмы также используются для декорирования и украшения различных предметов, таких как светильники и хрустальные изделия. Они создают эффекты преломления света, которые придают предметам элегантный и блестящий вид.
Это только некоторые примеры использования призм. Они обладают широким спектром применения и играют важную роль в различных областях науки, искусства и техники.
Призмы в геометрии 10 класс: изучение и применение

Изучение призм включает в себя изучение их свойств, формулы для вычисления площади поверхности и объема, а также основные характеристики призм. Это важная информация для решения различных геометрических задач и задач из реального мира.
Призмы играют значительную роль в различных областях жизни, таких как архитектура, строительство, дизайн и другие. Их формы и свойства могут быть использованы для создания различных предметов, как например, упаковки, конструкций и искусственных объектов.
Изучение призм в 10 классе поможет ученикам развить навыки в геометрии, а также понять, как применять геометрические концепции на практике. Знание о призмах позволит ученикам решать сложные геометрические задачи, а также анализировать и характеризовать различные фигуры в трехмерном пространстве.
Изучение призм в геометрии 10 класса открывает двери в мир трехмерной геометрии и позволяет ученикам углубить свои знания в этой области. Это поможет им лучше понять различные геометрические концепции и их применение. Изучение призм является важным шагом в математическом образовании и может послужить основой для дальнейшего изучения более сложных геометрических фигур и концепций.



