Среднее арифметическое является одним из наиболее распространенных и простых способов измерить характеристики группы данных. Это основной показатель, который используется для определения среднего значения величины. Однако, в реальности, идеальное среднее арифметическое часто недоступно. И здесь вступает в игру понятие погрешности, которое позволяет определить величину отклонения от истинного значения.
Погрешность среднего арифметического является мерой разброса или неточности данных, которые были взяты для вычисления среднего значения. Она представляет собой разность между средним арифметическим и истинным значением. Погрешность может быть положительной или отрицательной, в зависимости от направления отклонения.
Измерение погрешности среднего арифметического позволяет узнать, насколько точным может быть среднее значение в определенной выборке данных. Чем меньше погрешность, тем ближе среднее арифметическое к истинному значению. Однако, важно помнить, что погрешность является неизбежной частью измерений и необходимо учитывать ее в анализе данных.
Погрешность среднего арифметического: основные принципы

Однако для оценки достоверности полученного результата необходимо учитывать погрешность среднего арифметического. Погрешность возникает из-за различных случайных факторов, влияющих на значения данных.
Основным принципом погрешности среднего арифметического является то, что она учитывает разброс значений в наборе данных. Чем больше разброс, тем выше погрешность.
Для оценки погрешности среднего арифметического используется стандартное отклонение либо среднеквадратическое отклонение. Оно позволяет определить, насколько среднее арифметическое отклоняется от среднего значения набора данных.
Примером может служить следующая ситуация: у нас есть данные о средней температуре воздуха за неделю. Среднее арифметическое будет равно сумме всех значений за неделю, поделенной на 7 (количество дней). Однако, наша оценка может быть неточной из-за погрешности. Для определения погрешности необходимо вычислить стандартное отклонение, которое позволит учесть все различия в температуре каждого дня.
Таким образом, погрешность среднего арифметического является важной характеристикой, позволяющей оценить достоверность полученного результата. Она учитывает разброс значений в наборе данных и позволяет определить, насколько среднее арифметическое отклоняется от среднего значения.
Что представляет собой погрешность среднего арифметического?
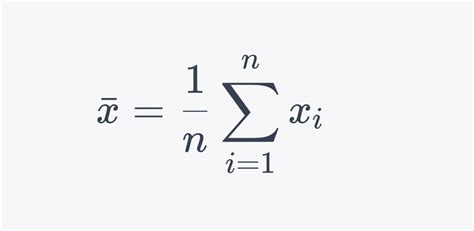
Погрешность среднего арифметического выражается в виде диапазона, в котором вероятно лежит реальное значение среднего с определенным уровнем доверия. Она может быть положительной или отрицательной величиной и указывает на возможность отклонения среднего значения от истинного значения.
Погрешность среднего арифметического зависит от количества данных, используемых для его вычисления, и дисперсии (разброса) этих данных. Чем больше данных и чем меньше разброс, тем меньше погрешность среднего арифметического.
Для оценки погрешности среднего арифметического используются стандартное отклонение и стандартная ошибка. Стандартное отклонение измеряет разброс данных относительно среднего значения, а стандартная ошибка представляет собой оценку погрешности среднего арифметического на основе стандартного отклонения и объема выборки.
Как рассчитывается погрешность среднего арифметического?

Погрешность среднего арифметического = среднеквадратичное отклонение (стандартное отклонение) / корень из количества измерений
Для расчета погрешности сначала необходимо найти среднеквадратичное отклонение, которое определяет разброс значений вокруг среднего. Затем среднеквадратичное отклонение делится на корень из количества измерений, чтобы привести результат к погрешности на одно измерение.
Погрешность среднего арифметического обычно представлена в виде числа с указанием единиц измерения и уровня значимости. Большое значение погрешности указывает на низкую точность данных, в то время как маленькое значение говорит о высокой точности.
Пример расчета погрешности среднего арифметического:
Допустим, у нас есть набор из 5 измерений: 10, 12, 14, 16, 18. Сначала найдем среднее арифметическое:
Среднее = (10 + 12 + 14 + 16 + 18) / 5 = 14
Затем найдем среднеквадратичное отклонение:
(10-14)² + (12-14)² + (14-14)² + (16-14)² + (18-14)² = 20
Среднеквадратичное отклонение = √(20/5) = 2
И, наконец, расчитаем погрешность среднего арифметического:
Погрешность среднего арифметического = 2 / √5 ≈ 0.89
Таким образом, погрешность среднего арифметического для данного набора данных составляет около 0.89.
Примеры погрешности среднего арифметического на практике

Погрешность среднего арифметического может возникать во множестве реальных ситуаций и иметь разные причины. Рассмотрим несколько примеров, где погрешность может влиять на результаты расчетов:
Пример 1: Измерение времени выполнения задачи компьютером
Предположим, что нам нужно оценить среднее время выполнения определенной задачи компьютером. Мы запускаем задачу несколько раз и измеряем время выполнения каждого запуска. Затем мы вычисляем среднее арифметическое, чтобы получить оценку среднего времени выполнения задачи. Однако, измерения могут содержать погрешности в виде случайных ошибок или систематических искажений. Погрешность измерения может привести к неправильной оценке среднего времени выполнения задачи, влияя на дальнейшие решения или оценки.
Пример 2: Расчет средней оценки студентов
Пример 3: Оценка среднего времени пребывания пациента в больнице
Рассмотрим ситуацию, когда мы хотим оценить среднее время пребывания пациента в больнице. Мы записываем время, которое каждый пациент проводит в больнице, и затем вычисляем среднее арифметическое для всех пациентов. Однако, могут возникать различные источники погрешности, такие как неправильная запись времени, неконтролируемые переменные, влияющие на время пребывания (например, осложнения после операции) и иные факторы, которые могут исказить реальное среднее время пребывания пациентов в больнице. Погрешность в оценке среднего времени пребывания пациентов может быть значительной и влиять на принятие решений о планировании ресурсов больницы и оценке эффективности работы медицинского персонала.
| Пример | Погрешность |
|---|---|
| Измерение времени выполнения задачи компьютером | Случайные ошибки, систематические искажения |
| Расчет средней оценки студентов | Ошибки при вводе оценок, субъективность оценки преподавателя, естественная изменчивость результатов студентов |
| Оценка среднего времени пребывания пациента в больнице | Неправильная запись времени, неконтролируемые переменные, влияющие на время пребывания |



