Площадь – это понятие, которое помогает определить, сколько площади занимает какая-либо фигура на плоскости. Для 3 класса важно понимать, как найти площадь простой фигуры, такой как квадрат. Квадрат – это геометрическая фигура, у которой все стороны равны между собой, а углы прямые. Площадь квадрата можно вычислить, зная длину одной его стороны.
Способ расчета площади квадрата прост: нужно умножить длину одной стороны на саму себя. Если, например, сторона квадрата равна 5 сантиметрам, то площадь квадрата будет равна 5 умножить на 5, то есть 25 квадратных сантиметров.
Примеры:
Пример 1: Рассмотрим квадрат со стороной 3 сантиметра. Чтобы вычислить его площадь, нужно умножить 3 на 3. Получаем, что площадь квадрата равна 9 квадратных сантиметров.
Пример 2: Представим себе квадратный стол. Если сторона стола равна 50 сантиметрам, то площадь стола будет равна 2500 квадратных сантиметров.
Зная, как вычислять площадь квадрата, вы сможете легко решать задачи, связанные с этой фигурой. Ученики третьего класса могут использовать этот навык для решения домашних и классных заданий по геометрии. Помните, что площадь квадрата можно вычислить, зная только длину одной его стороны.
Что такое площадь квадрата
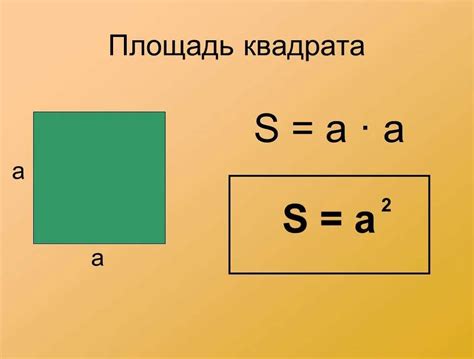
Площадь = сторона × сторона
Здесь "сторона" - длина одной из сторон квадрата. Если сторона квадрата равна, например, 5 единицам, то его площадь будет равна 5 единиц × 5 единиц = 25 квадратным единицам. Площадь измеряется в квадратных единицах, таких как квадратные метры (м²) или квадратные сантиметры (см²).
Площадь квадрата является мерой его поверхности и помогает нам определить, насколько большой или маленькой является эта фигура. Она может использоваться для решения различных задач: вычисления расхода материала для облицовки пола или стен, определения площади поля или участка земли, а также для оценки площади помещений или объектов в архитектуре и строительстве.
Рассчитывать площадь квадрата очень просто и требует только знания длины одной из его сторон. Зная эту величину, мы можем легко определить площадь квадрата по формуле. Важно помнить, что все стороны квадрата имеют одинаковую длину, поэтому для расчета площади нам достаточно знать только значение одной из сторон.
Определение и основные понятия

Основные понятия, связанные с площадью квадрата:
- Сторона квадрата: это отрезок, соединяющий две противоположные вершины квадрата. Все стороны квадрата равны между собой.
- Диагональ квадрата: это отрезок, соединяющий две противоположные вершины квадрата.
- Формула для вычисления площади: площадь квадрата равна квадрату длины его стороны. Формула выглядит так: S = a², где S - площадь, а - длина стороны.
Например, если сторона квадрата равна 5 сантиметров, то его площадь будет 25 квадратных сантиметров (5² = 25).
Понимание площади квадрата важно не только для учебы, но и для повседневной жизни. Например, зная площадь квартиры, можно определить, сколько мебели поместится в комнату или сколько обоев необходимо для оклейки стен.
Примеры расчета площади квадрата

Рассмотрим несколько примеров для понимания расчета площади квадрата.
| Сторона квадрата (см) | Площадь квадрата (см2) |
|---|---|
| 2 | 4 |
| 5 | 25 |
| 7 | 49 |
Из таблицы видно, что площадь квадрата считается путем умножения длины одной его стороны на саму себя.
Например, если сторона квадрата равна 2 сантиметра, то его площадь будет 2 умножить на 2, то есть 4 квадратных сантиметра.
Таким образом, с помощью этой формулы мы можем легко и быстро вычислить площадь квадрата для любого значения его стороны.
Упражнения для 3 класса

- Упражнение "Построение квадрата". Преподаватель может дать ученикам задание нарисовать квадраты разных размеров на листе бумаги, используя линейку и карандаш. Затем ученики могут сравнить размеры своих квадратов и догадаться, что у всех квадраты имеют одинаковую сторону.
- Упражнение "Поиск квадратов". Преподаватель может показать ученикам различные предметы в классе и попросить их найти предметы, которые имеют форму квадрата. Ученики должны подойти к этому упражнению со знанием, что все стороны квадрата равны.
- Упражнение "Раскраска квадратов". Преподаватель может дать ученикам черно-белую картинку с несколькими квадратами и попросить их раскрасить каждый квадрат определенным цветом. Это позволит ученикам лучше визуализировать квадраты и понять их форму.
- Упражнение "Игра в квадраты". Преподаватель может поделить класс на команды и дать каждой команде задание нарисовать как можно больше квадратов за ограниченное время. Ученики должны быть аккуратными и рисовать квадраты одинакового размера.
Эти упражнения помогут ученикам 3 класса развить понимание и навыки работы с площадью квадрата, а также сделают обучение более интересным и взаимодейственным.



