В геометрии перпендикуляр - это особый вид отношений между объектами. Два отрезка, прямых или плоскостей считаются перпендикулярными, если они образуют прямой угол друг с другом. Понятие перпендикуляра тесно связано с параллельными прямыми и плоскостями, и оно находит широкое применение не только в геометрии, но и в других науках и областях знаний.
Основные свойства перпендикуляра можно выразить следующим образом:
- Перпендикулярность двух объектов означает, что они образуют прямой угол в точке пересечения.
- Перпендикуляр делит прямой угол на два равных угла. Таким образом, угол, образованный перпендикуляром и одной из параллельных прямых или плоскостей, является прямым.
- Перпендикулярные прямые не пересекаются. Если две прямые перпендикулярны, то они не пересекаются ни в одной точке.
Примеры перпендикуляров можно найти в повседневной жизни и в различных областях. Например, на улицах города можно заметить перпендикулярное расположение улиц, которое образуется в результате построения кварталов. Также, перпендикулярные линии используются при строительстве, дизайне и изготовлении предметов. Понимание и применение понятия перпендикуляра является важной составляющей геометрической грамотности и позволяет лучше понимать пространственные отношения.
Перпендикуляр в геометрии: определение и свойства

Перпендикуляр имеет несколько свойств, которые помогают в его определении и решении геометрических задач. Вот некоторые из них:
1. Прямой угол: Перпендикулярные отрезки, прямые или плоскости формируют прямой угол. Прямой угол равен 90 градусам и является самым часто встречающимся видом угла в геометрии.
2. Взаимная перпендикулярность: Если две прямые перпендикулярны третьей прямой, то они также будут перпендикулярны друг другу. Это свойство позволяет находить перпендикулярные прямые и плоскости, используя уже известные.
3. Геометрические построения: Перпендикулярность является ключевым элементом во многих геометрических построениях, таких как построение серединного перпендикуляра или проведение перпендикуляра из точки на прямую.
4. Пересечение с векторами: Если перпендикуляр пересекается с векторами, то он разделяет их на две группы, принадлежащие к двум разным направлениям. Это свойство используется, например, при определении отрезков, находящихся под прямым углом друг к другу.
Понимание перпендикуляра и его свойств играет важную роль в геометрии и помогает в решении различных геометрических задач. Использование данных свойств позволяет строить фигуры, проводить линии под определенными углами и находить взаимосвязь между различными элементами геометрических фигур.
Что такое перпендикуляр в геометрии?

Перпендикулярные линии можно проиллюстрировать, нарисовав две прямые, которые касаются друг друга под прямым углом. Пересечение этих линий образует точку, называемую точкой пересечения. Перпендикуляр также может быть определен как линия, указывающая направление падения силы тяжести.
Перпендикулярные линии имеют несколько важных свойств. Одно из них состоит в том, что они имеют одинаковую длину, так как они образуют прямой угол. Кроме того, любой угол, образованный перпендикуляром с другой линией, будет равен 90 градусам.
Установление перпендикулярности между двумя линиями может быть полезно при измерении расстояний, построении прямых углов и решении различных геометрических задач. Например, использование перпендикуляра может помочь определить точку, которая находится на равном расстоянии от двух линий или построить прямую, проходящую через заданную точку и перпендикулярную другой прямой.
| Примеры перпендикулярных линий: |
|---|
| 1. Вертикальные линии, например, стены здания. Они перпендикулярны горизонтальному земле. |
| 2. Горизонтальные линии, например, пол. Они перпендикулярны вертикальной оси. |
| 3. Диагонали квадрата или прямоугольника, которые пересекаются и создают прямые углы. |
| 4. Линия, проведенная между центром окружности и любой ее точкой на окружности. |
Изучение перпендикулярности позволяет углубить понимание геометрии и применять это знание в различных ситуациях – от повседневных задач до сложных математических проблем.
Примеры использования перпендикуляра в геометрии
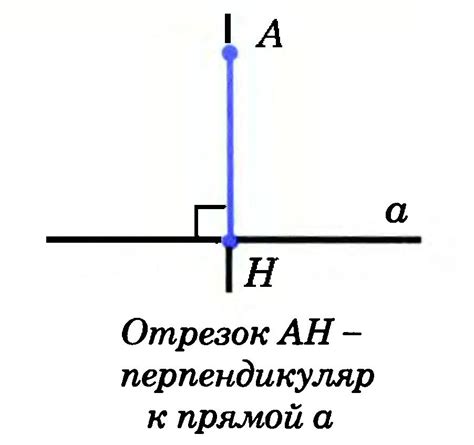
1. Построение прямого угла: Перпендикуляр используется для построения прямого угла. Для этого берется отрезок прямой и через один из его концов проводится перпендикуляр, который пересекает эту прямую. В точке пересечения образуется прямой угол, равный 90 градусам.
2. Построение отрезка, перпендикулярного другому отрезку: Если нужно построить отрезок, перпендикулярный данному отрезку, можно использовать следующую процедуру: с одного из концов данного отрезка проводится дуга, а затем с другого конца – другая дуга, радиус которой равен радиусу первой дуги. Точка пересечения дуг будет центром окружности, а отрезок, соединяющий его с начальным отрезком, будет перпендикулярен к нему.
3. Решение задач по координатной плоскости: В геометрии с использованием координатной плоскости перпендикуляр используется для решения различных задач, например, для определения точек пересечения двух прямых или для нахождения углов между прямыми.
4. Построение треугольника: Перпендикуляр может использоваться для построения треугольника с определенным углом. Например, если известна одна из сторон и угол между этой стороной и перпендикуляром, то можно построить треугольник, используя эти данные.
Все эти примеры демонстрируют важность перпендикуляра в геометрии и широкий спектр его применений.



