В геометрии существует несколько основных понятий, которые помогают нам описать и понять пространство и его свойства. Среди них - отрезок, прямая, луч и дополнительные лучи. Эти термины являются базовыми для понимания геометрических форм и их взаимодействия.
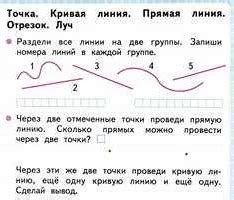
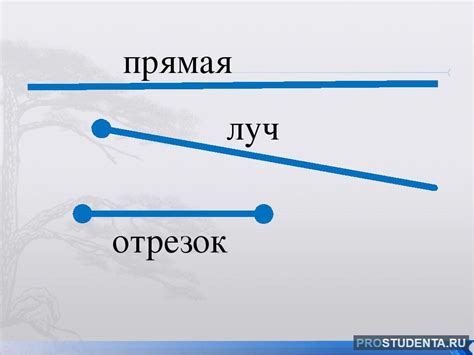
Отрезок - это непрерывная линия, которая соединяет две точки. Он имеет фиксированную длину и может быть представлен на плоскости или в пространстве. Отрезок обычно обозначается двумя точками на концах, например, AB. Длина отрезка вычисляется как расстояние между его конечными точками.
Прямая - это бесконечный набор точек, которые расположены в одном направлении. Она не имеет начала или конца и может быть представлена в виде прямой линии без стрелок на концах. Прямая обозначается одной буквой, например, l. Прямая также может быть определена двумя точками, через которые она проходит.
Луч - это часть прямой, которая имеет начало, но не имеет конца. Луч может распространяться только в одном направлении и иметь бесконечную длину. Луч обозначается одной буквой с знаком над ней, указывающим на направление, например, λ или AB→. Луч начинается в точке A и распространяется вдоль прямой в направлении, указанном стрелкой.
Дополнительные лучи - это два луча, которые продолжаются в обратном направлении от заданной точки на прямой или луче. Они образуются при расширении прямой или луча за его пределы. Дополнительные лучи обозначаются двумя буквами с надстрочными символами над ними, например, BA⇵ и BA↓. Они показывают направление от заданной точки до бесконечности в обратных направлениях.
Определение и понимание этих геометрических объектов помогают нам анализировать формы, строить модели и решать задачи в различных областях, включая инженерию, архитектуру и физику. Использование отрезков, прямых, лучей и дополнительных лучей позволяет нам точно определять и описывать различные геометрические формы в нашем окружении.
Отрезок: определение и примеры
Пример 1: Рассмотрим отрезок АВ на числовой прямой. Начало отрезка А соответствует точке -2, а конец отрезка В – точке 4. Длина данного отрезка равна 6, так как расстояние между -2 и 4 равно 6.
Пример 2: В геометрии мы можем рассматривать и отрезки без числовых значений. Например, отрезок МН имеет начало в точке М и конец в точке Н. Точные координаты или значения не важны, главное – наличие начала и конца.
Отрезки используются в различных задачах, как в геометрии, так и в физике, экономике и других науках. Они могут быть использованы для измерения расстояний, построения фигур и моделирования различных процессов.
Что такое отрезок в геометрии
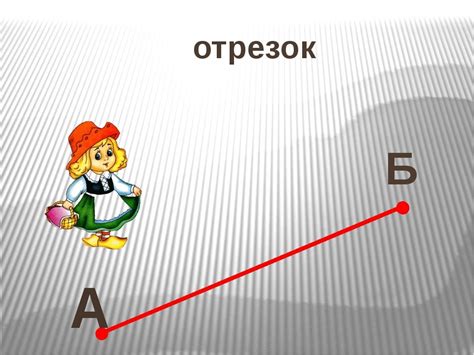
Отрезок обозначается двумя точками, расположенными на этом отрезке, например, AB, CD или EF. Точки, которые ограничивают отрезок, называются его концами. Обычно начальная точка отрезка представлена первой буквой в обозначении отрезка, а конечная точка - второй буквой.
Отрезки могут быть разными по длине. Если конечные точки отрезка совпадают, то получается вырожденный отрезок, который обычно называют точкой.
Отрезки используются в геометрии для измерения расстояний между точками, а также для построения геометрических фигур и решения различных задач.
Примеры отрезка
1. Отрезок AB: Обозначим точку A и точку B на прямой. Отрезок AB будет представлять собой отрезанную часть прямой между точками A и B, включая эти точки.
2. Отрезок CD: Возьмем другие две точки C и D на той же прямой. Отрезок CD будет представлять собой отрезанную часть прямой между этими точками, включая их.
3. Отрезок EF: Рассмотрим точки E и F на прямой. Отрезок EF будет иметь начало в точке E и конец в точке F.
Отрезки могут быть разной длины и положения на прямой. Они могут пересекаться или быть параллельными друг другу.
Прямая: определение и особенности
Особенности прямой:
| Определение | Прямая определяется двумя различными точками на ней. Любые две точки на прямой можно соединить отрезком. |
| Бесконечность | Прямая не имеет начала и конца - она продолжается в обе стороны до бесконечности. |
| Единственность | Через любые две точки в пространстве можно провести только одну прямую. |
| Прямая и отрезок | Прямая может рассматриваться как бесконечно длинный отрезок. |
Пример использования прямой:
Представим себе следующую ситуацию: мы хотим составить рисунок домика на листе бумаги. Для этого мы рисуем две прямые линии, которые пересекаются под углом 90 градусов. Эти прямые линии являются стенами домика и не имеют начала и конца. Таким образом, мы нарисовали прямую.
Что такое прямая линия?
Прямую линию можно определить как наименьшую дистанцию между двумя точками, также называемыми начальной и конечной точкой. Важно отметить, что прямую можно продолжать в обоих направлениях до бесконечности.
Прямая линия обычно обозначается одной буквой, например, "l" или "m", и может быть представлена в виде отрезка или луча на графике.
| Элемент | Описание | Пример |
|---|---|---|
| Отрезок | Часть прямой линии между двумя точками | AB |
| Луч | Начинается в одной точке и расширяется до бесконечности в одном направлении | AC |
| Дополнительные лучи | Начинаются в одной точке и расширяются до бесконечности в двух направлениях | AD и AE |
Прямая линия является одним из основных понятий геометрии и широко используется в математике, физике и других науках. Она помогает нам понять и описывать пространственные отношения и взаимодействия объектов в нашем мире.
Основные свойства прямой
1. Бесконечная протяженность: Прямая продолжается в обе стороны без ограничения, без каких-либо конечных точек. Она не имеет начала или конца.
2. Равенство расстояний: Любые две точки на прямой имеют одинаковое расстояние от некоторой другой точки.
3. Прямая и все ее отрезки: Прямая может быть разделена на отрезки двумя способами. А именно, каждый отрезок прямой имеет начало и конец, которые являются точками на этой же прямой.
4. Прямая и угол: Прямая может определять углы. Если две прямые пересекаются в точке, они образуют два угла, называемые вертикальными углами. Вертикальные углы равны между собой.
5. Кратчайшее расстояние: Прямая является кратчайшим расстоянием между двумя точками. Из любой точки на прямой можно нарисовать перпендикулярную линию, которая будет иметь наименьшее расстояние до точки.
6. Непрерывность: Если прямая разрезается на две части, то она становится непрерывной кривой, что означает, что ее можно пройти от одной точки до другой, не отрываясь.
Это основные свойства прямой, которые делают ее важной и используемой в геометрии и других науках.
Луч: понятие и использование

Луч используется для описания направления движения из одной точки. Он может использоваться для построения углов, определения трассы света, нахождения границ тел и многое другое.
Например, в геометрическом построении угла, одна сторона может представлять собой луч, который выходит из вершины угла. Луч может указывать направление движения света или лучи солнца.
В физике лучи также используются для описания направления распространения электромагнитных волн и других видов излучения. Лучи света, альфа-лучи и бета-лучи являются примерами такого использования.
Таким образом, понимание луча и его использование в геометрии и физике имеет широкий спектр применения, что делает его важным понятием для изучения и практического применения в различных областях.



