Общий знаменатель дробей - это знаменатель, который имеют все дроби в группе, когда они записываются в виде десятичных дробей. Точнее говоря, это знаменатель, который является общим для всех дробей и позволяет сравнивать их или выполнять операции сложения, вычитания, умножения и деления.
Чтобы найти общий знаменатель дробей, сначала необходимо выписать все знаменатели каждой из дробей. Затем нужно определить наименьшее общее кратное (НОК) всех знаменателей. Это число и будет являться общим знаменателем дробей.
Например, если у нас есть дроби 1/2, 3/4 и 2/3, то знаменатели этих дробей равны 2, 4 и 3 соответственно. Наименьшее общее кратное этих чисел равно 12, поэтому 12 - это общий знаменатель для всех трех дробей.
Общий знаменатель дробей является важным понятием в математике, поскольку позволяет производить операции с дробями и сравнивать их. Используя общий знаменатель, мы можем сложить, вычесть, умножить или разделить дроби, как если бы они были целыми числами. Это значительно упрощает работу с дробями и позволяет нам легко решать задачи, связанные с дробями.
Общий знаменатель дробей: правила, примеры, объяснение

Существует несколько правил, которые помогают нам найти общий знаменатель для дробей:
- Если знаменатели двух дробей равны, то общим знаменателем будет этот знаменатель.
- Если знаменатели дробей могут быть представлены в виде произведения общего знаменателя и некоторого числа, то общим знаменателем будет это произведение.
- Если знаменатели не могут быть представлены в виде произведения общего знаменателя и некоторого числа, то общим знаменателем будет их наименьшее общее кратное (НОК).
После нахождения общего знаменателя, нам необходимо привести все дроби к этому знаменателю. Для этого мы домножаем числитель и знаменатель каждой дроби на такое число, чтобы получился общий знаменатель.
Пример:
У нас есть две дроби: 1/4 и 2/3. Для нахождения общего знаменателя мы можем использовать третье правило и вычислить НОК знаменателей, который равен 12. Теперь мы домножаем числитель и знаменатель первой дроби на 3, а числитель и знаменатель второй дроби на 4. Получается:
1/4 = 3/12
2/3 = 8/12
Теперь у нас есть две дроби с общим знаменателем 12, и мы можем выполнять операции с ними, например, сложение или вычитание.
Общий знаменатель дробей является важным понятием в арифметике дробей, и его использование помогает упростить выполнение операций с дробями.
Определение общего знаменателя дробей

Чтобы найти общий знаменатель для двух дробей, необходимо найти наименьшее общее кратное (НОК) их знаменателей. В результате этой операции получается новый знаменатель, который становится общим для обеих дробей.
Для примера, рассмотрим следующие дроби: 3/4 и 2/5. Знаменатели этих дробей составляют 4 и 5 соответственно. Наименьшее общее кратное этих чисел - 20. Поэтому общий знаменатель для этих дробей равен 20. Используя этот общий знаменатель, дроби могут быть приведены к эквивалентным дробям: 3/4 = 15/20 и 2/5 = 8/20.
Таким образом, общий знаменатель дробей позволяет выполнять арифметические операции с этими дробями, такие как сложение, вычитание, умножение и деление, с учетом их истинных значений и отношений.
Правила нахождения общего знаменателя дробей

Существует несколько правил для нахождения общего знаменателя дробей:
- Если у дробей уже есть общий знаменатель, то он и будет общим знаменателем для данного набора дробей.
- Если в наборе дробей присутствует дробь со знаменателем 1, то общим знаменателем будет произведение всех знаменателей.
- Если в наборе дробей присутствует дробь со знаменателем, являющимся произведением различных простых чисел, то общим знаменателем будет произведение всех знаменателей.
- Если в наборе дробей присутствуют дроби со знаменателями, имеющими общие простые множители, то общим знаменателем будет произведение всех знаменателей, включая каждый простой множитель не более одного раза.
- Если в наборе дробей присутствует дробь со знаменателем, являющимся наименьшим общим кратным всех знаменателей, то общим знаменателем также будет это наименьшее общее кратное.
Применение правил нахождения общего знаменателя дробей позволяет упростить операции с дробями и упрощать их запись в удобной и понятной форме.
Примеры вычисления общего знаменателя дробей

Общий знаменатель дробей вычисляется путем нахождения наименьшего общего кратного знаменателей данных дробей. Рассмотрим несколько примеров для наглядности.
Пример 1:
Вычислим общий знаменатель для дробей 2/3 и 3/4:
Знаменатели данных дробей равны 3 и 4. Для нахождения наименьшего общего кратного этих чисел можно воспользоваться следующей формулой:
НОК(3, 4) = (3 * 4) / НОД(3, 4)
Для вычисления НОД(3, 4) воспользуемся алгоритмом Евклида:
НОД(3, 4) = НОД(4, 3) = НОД(1, 3) = 1
Теперь вычислим НОК(3, 4) с использованием найденного НОД:
НОК(3, 4) = (3 * 4) / 1 = 12
Таким образом, общий знаменатель для дробей 2/3 и 3/4 равен 12.
Пример 2:
Вычислим общий знаменатель для дробей 1/5 и 2/7:
Знаменатели данных дробей равны 5 и 7. Применим ту же формулу для вычисления НОК и НОД:
НОД(5, 7) = НОД(7, 5) = НОД(2, 5) = 1
НОК(5, 7) = (5 * 7) / 1 = 35
Таким образом, общий знаменатель для дробей 1/5 и 2/7 равен 35.
Пример 3:
Вычислим общий знаменатель для дробей 3/8, 5/6 и 1/4:
Знаменатели данных дробей равны 8, 6 и 4. Применим формулу для вычисления НОК и НОД:
НОД(8, 6, 4) = НОД(8, НОД(6, 4)) = НОД(8, 2) = 2
НОК(8, 6, 4) = (8 * 6 * 4) / 2 = 48
Таким образом, общий знаменатель для дробей 3/8, 5/6 и 1/4 равен 48.
Вычисление общего знаменателя дробей позволяет сравнивать и складывать дроби с разными знаменателями. Это важное понятие помогает в работе с дробями и находит применение в различных математических задачах.
Объяснение важности общего знаменателя дробей
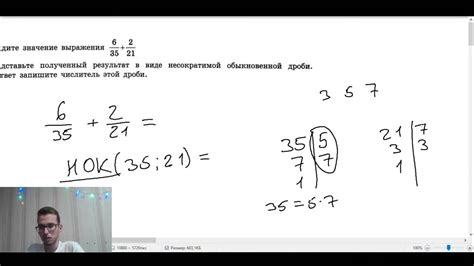
Когда у нас есть две дроби с разными знаменателями, для выполнения операций с ними необходимо привести их к общему знаменателю. Общий знаменатель будет наименьшим общим кратным исходных знаменателей.
Приведение дробей к общему знаменателю позволяет нам удобно производить арифметические операции с ними, такие как сложение, вычитание, умножение и деление. Без общего знаменателя решение таких задач становится гораздо сложнее и менее точным.
Например, если у нас есть дроби 3/4 и 1/8, чтобы сложить их, мы должны привести их к общему знаменателю. В данном случае, наименьшим общим знаменателем будет 8, поскольку 8 является кратным и 4, и 8. Получившиеся дроби будут: 6/8 и 1/8. Теперь мы можем их сложить и получить результат 7/8.
Важность общего знаменателя дробей заключается в том, что он позволяет нам проводить точные и однородные операции с дробями. Без него мы бы не смогли сравнивать и складывать дроби с разными знаменателями и были бы ограничены в решении множества математических задач.
Что делать, когда общий знаменатель дробей не найден

Иногда при работе с дробями может возникнуть ситуация, когда общий знаменатель для нескольких дробей не удается найти сразу. Здесь мы рассмотрим несколько способов решения этой проблемы.
- Использование наименьшего общего кратного (НОК)
- Умножение знаменателей
- Приведение дробей к эквивалентным
Один из способов найти общий знаменатель для дробей - это использование наименьшего общего кратного (НОК) их знаменателей. НОК является наименьшим числом, которое кратно всем знаменателям. Если знаменатели дробей уже являются общими кратными, то этот метод можно использовать напрямую. В противном случае, необходимо найти НОК и затем привести все дроби к этому знаменателю.
Если у дробей нет общего кратного, можно попробовать умножить их знаменатели друг на друга. Это поможет получить новые знаменатели, которые могут оказаться общими для всех дробей. После этого необходимо привести все дроби к этим новым знаменателям.
Если по какой-то причине не удается найти общий знаменатель с использованием НОК или умножением знаменателей, можно попытаться привести дроби к эквивалентным, то есть дроби с одинаковыми знаменателями. Для этого необходимо выполнить операции с числителями и получить новые дроби с общим знаменателем.
Помните, что поиск общего знаменателя может потребовать дополнительных вычислений и анализа, особенно если имеется большое количество дробей или сложная структура уровней знаменателей. Однако правильное нахождение общего знаменателя является важным шагом для проведения операций с дробями, таких как сложение, вычитание или умножение.
Чтобы найти общий знаменатель двух или более дробей, нужно найти наименьшее общее кратное их знаменателей. Для этого можно использовать методы факторизации или просто просмотреть все числа до двух знаменателей и выбрать наименьшее число, которое делится без остатка на оба знаменателя.
После нахождения общего знаменателя, каждую дробь нужно привести к этому знаменателю путем умножения числителя и знаменателя на соответствующий множитель.
Например, если есть две дроби: 2/3 и 1/4, общим знаменателем будет 12 (наименьшее общее кратное 3 и 4). Чтобы привести 2/3 к знаменателю 12, нужно умножить числитель и знаменатель на 4. Таким образом, 2/3 станет равной 8/12. Аналогично, чтобы привести 1/4 к знаменателю 12, нужно умножить числитель и знаменатель на 3. Таким образом, 1/4 станет равной 3/12. Теперь можно производить операции с этими дробями, такие как сложение или вычитание.
Понимание общего знаменателя очень полезно при работе с дробями, поскольку позволяет производить различные операции с дробями и упрощать выражения.



