Модуль – это одно из основных понятий в математике, с которым знакомятся ученики уже в 7 классе. Модулем числа называется его абсолютная величина, то есть число без знака. Важно понимать, что модуль числа всегда является неотрицательным числом.
Для определения модуля числа a используется специальная запись: |a|. Если число a является положительным, то его модуль равен самому числу. Например, модуль числа 5 равен 5. Если число a является отрицательным, то его модуль равен числу без знака. Например, модуль числа -5 равен 5.
Модуль числа может использоваться для решения различных математических задач. Например, он может быть полезен при вычислении расстояния между двумя точками на числовой оси или при нахождении решений некоторых уравнений. Понимание модуля числа поможет ученикам более глубоко понять понятие абсолютной величины, которое является основой для дальнейшего изучения математики.
Понятие модуля

Другими словами, модуль числа – это его числовая величина, игнорируя его знак. Модуль числа обозначается символом |x|, где x - само число. Если число положительное или равно нулю, то модуль числа равен самому числу. Если число отрицательное, то модуль числа равен числу с обратным знаком.
Одно из основных применений модуля числа в математике - нахождение расстояния между двумя точками на числовой прямой. Например, если нужно найти расстояние между точками -3 и 5, то можно найти модули этих чисел и сложить их: |-3| + |5| = 3 + 5 = 8.
Определение и примеры

Например, модуль числа -5 это 5, так как расстояние от -5 до 0 равно 5. Модуль числа 3 равен 3, так как число 3 положительное и его расстояние от 0 равно 3.
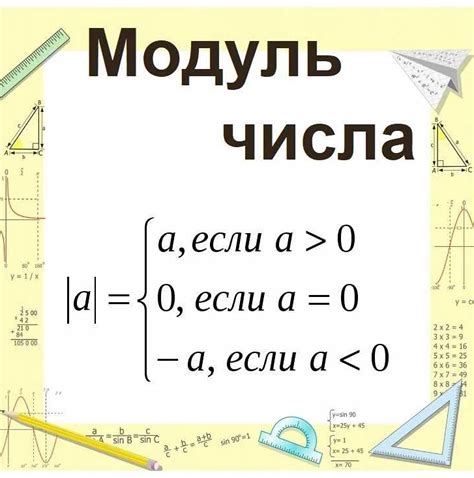
Модуль можно выразить формулой: |х| = х, если x ≥ 0; |х| = -х, если x < 0.
Свойства модуля

1. Модуль числа всегда неотрицателен: Независимо от значения числа, модуль всегда будет положительным или нулем. Например, модуль числа -5 равен 5.
2. Модуль равен нулю только для нуля: Модуль числа будет равен нулю только в том случае, если само число равно нулю. Например, модуль числа 0 равен 0.
3. Модуль суммы двух чисел не больше, чем сумма их модулей: Если взять модуль от суммы двух чисел, то он всегда будет меньше или равен сумме модулей этих чисел. Например, |a + b| ≤ |a| + |b|.
4. Модуль произведения двух чисел равен произведению их модулей: Если взять модуль от произведения двух чисел, то он будет равен произведению модулей этих чисел. Например, |a * b| = |a| * |b|.
5. Значение модуля слагаемого не зависит от его знака: Значение модуля числа не зависит от его знака. Например, модуль числа -3 равен модулю числа 3.
6. Модуль разности двух чисел не меньше, чем разность их модулей: Если взять модуль от разности двух чисел, то он всегда будет больше или равен разности модулей этих чисел. Например, |a - b| ≥ |a| - |b|.
Модуль и арифметические операции

Модуль можно использовать при выполнении арифметических операций. При сложении или вычитании чисел, модуль учитывает только их абсолютные значения.
Например, модуль суммы двух чисел равен сумме модулей этих чисел. Если модуль суммы чисел 8 и 3, то он равен модулю числа 11.
При умножении числа на модуль другого числа, результат будет равен модулю произведения этих чисел. Например, модуль произведения числа -3 и 4 равен модулю числа -12, то есть 12.
Модуль также используется при выполнении деления чисел. Модуль частного двух чисел равен частному модулей этих чисел. Например, если модуль деления числа 15 на -3, то он равен модулю числа -5.
Таким образом, модуль позволяет учитывать только абсолютные значения чисел при выполнении арифметических операций, игнорируя их знаки.
Модуль и координатная плоскость
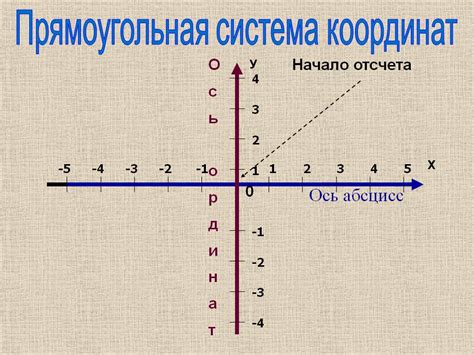
Как связан модуль числа с координатной плоскостью? В двумерной координатной плоскости каждая точка имеет свои координаты (x, y), где x - горизонтальная ось, а y - вертикальная ось. Модуль числа можно интерпретировать как расстояние от этой точки до начала координат (0, 0).
Например, если на координатной плоскости дана точка A с координатами (3, 4), то модуль числа 3 равен |3| = 3, а модуль числа 4 равен |4| = 4. Расстояние от точки A до начала координат будет равно √(3^2 + 4^2) = 5. Таким образом, модуль числа можно рассматривать как длину вектора, идущего от начала координат до точки с заданными координатами.
Также модуль числа может быть использован для определения расстояния между двумя точками на координатной плоскости. Если точки имеют координаты (x1, y1) и (x2, y2), то расстояние между ними можно найти по формуле √((x2 - x1)^2 + (y2 - y1)^2).
Использование модуля числа в математике помогает упростить вычисления и решение задач на координатной плоскости.
Модуль в уравнениях и неравенствах
Модуль может быть положительным или равным нулю: |x| ≥ 0, и только одно число – ноль - дает значение ноль.
Модуль встречается в решении уравнений и неравенств. Когда модуль стоит перед переменной, то решение делится на две части, и значения переменной с разными знаками модуля задаются двумя условиями.
В уравнении |x| = a решениями могут быть x=a и x=-a. То есть, число a и его симметричное относительно нуля значение -a.
В неравенстве |x| < a решениями могут быть x-a. То есть, числа, которые находятся между -a и a.
Решение уравнений и неравенств с модулем требует учета возможных вариантов для значения переменной в области модуля.
Практические примеры на модуль

Пример 1:
Допустим, у вас есть два числа: -5 и 5. Чтобы найти модуль числа, нужно взять его абсолютное значение, то есть убрать знак. Модуль числа -5 равен 5, а модуль числа 5 равен также 5.
Пример 2:
Предположим, у вас есть деталь абсолютных значений долга и кредита. Долг представлен отрицательным числом, а кредит - положительным числом. Если вы хотите найти общую сумму, то вам необходимо использовать модуль для превращения отрицательного числа долга в положительное. Например, если у вас есть долг -1000 и кредит 500, то общая сумма будет равна 500 + |-1000| = 500 + 1000 = 1500.
Пример 3:
Модуль также может быть использован для определения расстояния между двумя точками на числовой прямой. Например, чтобы найти расстояние между точками 3 и 10, нужно вычислить разность между этими точками и взять модуль от результата. В данном случае, расстояние будет равно |-10 - 3| = |-7| = 7.
Все эти примеры помогут вам лучше понять, как работает модуль в математике. Он может быть полезен во многих ситуациях, когда вам необходимо убрать знак числа или найти расстояние между точками. Запомните, что модуль числа всегда будет положительным или нулевым.



