В алгебре 10 класса модой называется такое число или набор чисел, которое встречается в данном наборе чаще всего. Мода позволяет нам определить наиболее часто встречающиеся значения в выборке и выделить их для дальнейшего анализа. Мода является одним из элементов статистики и играет важную роль в анализе данных.
Для нахождения моды в алгебре 10 класса необходимо выполнить несколько шагов. Во-первых, нужно составить таблицу значений, где будут указаны числа и их частота встречаемости. После этого следует определить, какое значение или значения встречаются наиболее часто. Если есть несколько чисел с одинаковой или максимальной частотой, то таких чисел может быть несколько.
Нахождение моды позволяет оценить наиболее типичные значения в выборке. Например, при изучении результатов теста по математике, модой может быть число, которое большинство учеников набрали. Это может указывать на наиболее сложные или популярные вопросы теста. Понимание моды и ее значения в алгебре 10 класса помогает в дальнейшем анализе и интерпретации данных, а также может использоваться для прогнозирования будущих результатов.
Основные понятия алгебры

Числа в алгебре могут быть натуральные (1, 2, 3, ...), целые (-3, -2, -1, 0, 1, 2, 3, ...), рациональные (дроби, такие как 1/2, 3/4, -2/7), иррациональные (корень из 2, π) и действительные (любое число на числовой прямой).
Переменные представляют собой символы, которые обозначают неизвестные или зависящие от контекста значения. Они используются для построения алгебраических выражений и уравнений. Чаще всего используются буквы (x, y, z), но также могут использоваться и другие символы.
Операции – это математические действия, которые выполняются над числами или переменными. Основные операции включают сложение, вычитание, умножение и деление. Они позволяют строить алгебраические выражения и решать алгебраические уравнения.
Алгебраические выражения представляют собой комбинации чисел, переменных и операций. Они могут быть составлены из одного или нескольких слагаемых, умножителей и степеней. Примеры алгебраических выражений: 3x + 2y, 4a^2 - b, 2(x + y).
Алгебраические уравнения – это равенства, содержащие неизвестные переменные. Они представляют собой уравнения, которые можно решить для определения значений переменных. Примеры алгебраических уравнений: 2x + 5 = 10, x^2 - 4 = 0.
Расчеты с переменными в алгебре

Один из основных методов работы с переменными в алгебре - замена переменных на числа и выполнение необходимых вычислений. Этот метод позволяет нам найти значение переменной и решить уравнение или неравенство.
Пример расчета с переменными:
- Задача: Найти значение переменной x, если известно, что x + 5 = 10.
- Решение: Заменим переменную x на число и выполним соответствующие вычисления.
x + 5 = 10
x = 10 - 5
x = 5 - Ответ: Значение переменной x равно 5.
Расчеты с переменными также позволяют нам решать уравнения с неизвестными коэффициентами. В таких случаях мы можем использовать алгебраические операции, чтобы изолировать переменную и найти ее значение.
Пример расчета с переменными и коэффициентами:
- Задача: Найти значение переменной x, если известно, что 2x - 3 = 7.
- Решение: Используем алгебраические операции, чтобы изолировать переменную.
2x - 3 = 7
2x = 7 + 3
2x = 10
x = 10 / 2
x = 5 - Ответ: Значение переменной x равно 5.
Расчеты с переменными в алгебре позволяют нам работать с неизвестными значениями и находить решения для различных математических задач. Они являются фундаментальным инструментом в алгебре и используются в различных областях науки, техники и экономики.
Решение уравнений и неравенств в алгебре
Для решения уравнений в алгебре используются различные методы. Один из наиболее распространенных методов - метод подстановки. Он заключается в последовательной замене переменных в уравнении и получении результата, который должен быть равен нулю. Если найденное значение переменной удовлетворяет условию равенства, то это и есть решение уравнения.
Также в алгебре используется метод факторизации, который позволяет разложить уравнение на множители и найти корни. Для решения линейных уравнений (уравнений первой степени) применяется метод замены переменных, где искомая переменная заменяется другой переменной, после чего решается полученное уравнение.
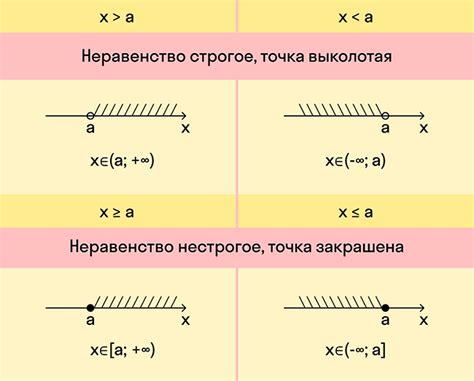
Решение неравенств в алгебре также осуществляется с помощью различных методов. Для решения линейных неравенств используется метод "отрезка". В этом методе задается отрезок числовой оси, на котором ищутся значения переменной, удовлетворяющие неравенству. Для решения квадратных неравенств применяется метод построения графика функции и анализа ее поведения.
Важно отметить, что при решении уравнений и неравенств в алгебре возможно получение не одного, а нескольких решений. Это связано с тем, что многие уравнения и неравенства имеют бесконечное множество решений или множество решений задается интервалами.
Графики функций в алгебре
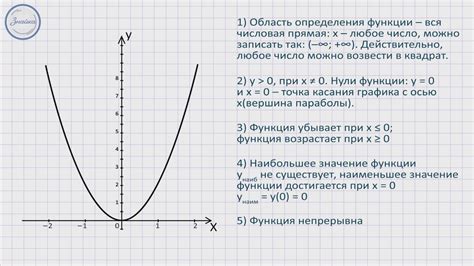
Графики функций занимают важное место в изучении алгебры. Они позволяют наглядно представить изменение значений функций в зависимости от аргумента и позволяют решать различные задачи, связанные с анализом функций.
График функции представляет собой изображение множества точек, координаты которых образуются путем подстановки различных значений аргумента в уравнение функции. В результате получается плоская кривая, которая может быть линией, окружностью, параболой и т.д., в зависимости от вида функции.
Графики функций могут быть полезны при решении уравнений, поиске экстремумов, определении области значений и множества определения функций, а также при анализе их свойств.
Для построения графика функции необходимо определить область значений, множество определения функции, а также выбрать различные значения аргумента и подставить их в уравнение функции. По полученным координатам точек можно построить график на координатной плоскости.
Построение графиков функций позволяет визуализировать алгебраические объекты и уравнения, что делает их более понятными и позволяет проводить различные аналитические и графические операции с функциями.



