Мнимая единица - это комплексное число, которое обозначается буквой i. Она является решением квадратного уравнения x^2 = -1. В математике, мнимая единица является одним из основных элементов комплексных чисел и играет важную роль в различных областях науки и техники.
Мнимая единица обладает уникальными свойствами. Во-первых, её квадрат равен -1, что дает основу для построения комплексных чисел. Во-вторых, мнимая единица обладает периодическими свойствами, что делает её полезным инструментом в анализе и моделировании периодических процессов. Например, в электротехнике, мнимая единица широко применяется для описания синусоидальных величин.
Мнимая единица также играет важную роль в геометрии комплексной плоскости. Она позволяет представлять комплексные числа как точки на плоскости и связывает алгебраическое и геометрическое представление комплексных чисел. Также, мнимая единица используется в теории вероятностей и физике, где она помогает в решении сложных задач и введении новых понятий.
Итак, мнимая единица - это неотъемлемый элемент математики, который играет важную роль в различных областях науки и техники. Она обладает уникальными свойствами и позволяет расширить наши математические возможности. Понимание мнимой единицы важно для работы с комплексными числами и открывает новые горизонты в познании мира.
Определение мнимой единицы

Мнимая единица обладает следующими свойствами:
- Мнимая единица возводится в квадрат, равный -1: i^2 = -1.
- Мнимая единица возводится в любую нечетную степень, равную сами себе с учетом знака: i^3 = -i, i^5 = -i, и т.д.
- Мнимая единица удовлетворяет свойству коммутативности: i*a = a*i, где a - любое действительное число.
Мнимые числа представляют собой комбинацию действительных и мнимых единиц и записываются в виде a + bi, где a и b – действительные числа, а i – мнимая единица. Комплексные числа можно складывать, вычитать, умножать и делить, что позволяет использовать их в различных областях науки и техники.
Мнимые числа и комплексные числа

Действительная часть комплексного числа представляет собой обычное действительное число. Мнимая часть комплексного числа обозначается буквой "i" и умножается на вещественное число, называемое мнимой единицей. Мнимая единица обладает свойствами, позволяющими проводить арифметические операции с комплексными числами.
Комплексные числа представляются в виде a + bi, где a - действительная часть, а bi - мнимая часть. Используя комплексные числа, можно выполнять операции сложения, вычитания, умножения и деления, а также получать корни квадратных уравнений, которые не имеют решения в области действительных чисел.
| Операция | Формула |
|---|---|
| Сложение | (a + bi) + (c + di) = (a + c) + (b + d)i |
| Вычитание | (a + bi) - (c + di) = (a - c) + (b - d)i |
| Умножение | (a + bi) * (c + di) = (ac - bd) + (ad + bc)i |
| Деление | (a + bi) / (c + di) = (ac + bd) / (c^2 + d^2) + (bc - ad)i / (c^2 + d^2) |
Мнимые числа и комплексные числа нашли широкое применение в различных областях науки и техники, таких как электроника, физика, теория сигналов и многих других. Они помогают решать задачи, которые не могут быть представлены только с помощью действительных чисел.
История открытия мнимой единицы

Понятие мнимой единицы в математике возникло в середине XVI века. На протяжении многих веков математики сталкивались с трудностями, связанными с вычислением корней некоторых уравнений. В некоторых случаях уравнения, такие как x^2 + 1 = 0, не имели решений среди действительных чисел. Эта проблема привлекла внимание математиков.
Впервые понятие мнимой единицы было введено и описано итальянским математиком Рафаэлем Бомбелли в его работе "Алгебра" в 1572 году. Он использовал букву "i" для обозначения мнимой единицы и впервые предложил систему комплексных чисел.
Однако идея комплексных чисел была довольно необычной и не была широко принята на первых порах. Они были слишком абстрактными и представляли собой что-то вроде "воображаемых" чисел. Вплоть до XVIII века мнимые числа вызывали сомнения и споры среди математиков.
Ситуация изменилась около середины XVIII века, когда математик Леонард Эйлер стал активно изучать комплексные числа и разработал формулу, известную как "формула Эйлера". Он показал, что мнимая единица можно представить в виде экспоненты:
e^(iπ) + 1 = 0
Эта формула принесла новое понимание мнимой единицы и положила начало развитию теории комплексных чисел. Открытие Эйлера стало ключевым моментом и открыло дверь к широкому применению мнимых чисел в различных областях математики и науки в целом.
Алгебраическое представление мнимой единицы

Чтобы понять алгебраическое представление мнимой единицы, необходимо знать о двух важных понятиях: комплексных числах и вещественной оси.
Комплексные числа - это числа вида a + bi, где a и b являются вещественными числами, а i - мнимая единица. Вещественная ось - это линия, на которой расположены все вещественные числа. Ось, перпендикулярная вещественной оси, называется мнимой осью, и на ней располагаются все комплексные числа, у которых вещественная часть равна нулю.
Алгебраическое представление мнимой единицы приходит из определения: i = √(-1). Это означает, что i является квадратным корнем из -1. Выражение a + bi, где a = 0, представляет комплексное число чисто на мнимой оси.
Мнимая единица также имеет интересное свойство: i^2 = -1. Это означает, что при возведении мнимой единицы в квадрат, мы получим -1. Это свойство является основой многих операций с комплексными числами.
Алгебраическое представление мнимой единицы играет важную роль в различных областях математики и физики, таких как электротехника, квантовая механика и теория сигналов. Понимание основных свойств и определений мнимой единицы является важным для изучения этих областей и решения математических проблем.
Геометрическое представление мнимой единицы
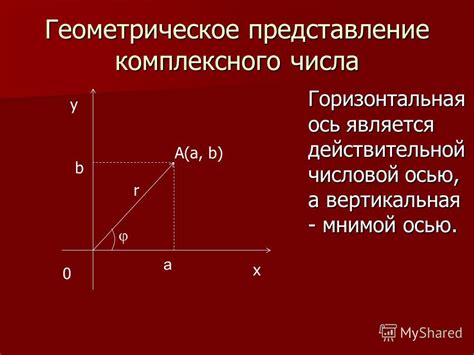
На комплексной плоскости мнимая единица располагается на оси oy и обозначается точкой i. Это означает, что мнимая единица имеет нулевую вещественную часть и единичную мнимую часть.
С помощью мнимой единицы можно задавать комплексные числа, которые имеют как вещественную, так и мнимую части. Комплексные числа могут представляться в виде a + bi, где a - вещественная часть, а b - мнимая часть.
Геометрическое представление мнимой единицы является основой для понимания комплексных чисел и играет важную роль в решении различных математических задач и приложениях.
Свойства мнимой единицы
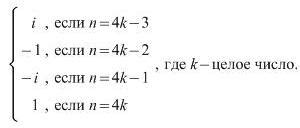
1. Квадрат мнимой единицы: Квадрат мнимой единицы равен -1, то есть i2 = -1. Это свойство обусловливает многие дальнейшие вычисления и применения мнимой единицы.
2. Множество комплексных чисел: Множество комплексных чисел можно представить в виде комбинаций действительных чисел (вещественных чисел) и мнимых чисел, где вещественная часть обозначается как Re, а мнимая часть - Im. Комплексное число записывается в виде a + bi, где a и b - вещественные числа.
3. Представление функций: Мнимая единица используется для представления различных функций в математике и физике. Например, синус, косинус и экспоненциальная функция могут быть записаны с использованием мнимой единицы.
4. Решение квадратных уравнений: Мнимая единица позволяет решать квадратные уравнения, которые имеют отрицательный дискриминант. Если в квадратном уравнении присутствует мнимая единица, то корни становятся комплексными числами.
5. Геометрическая интерпретация: Мнимая единица имеет геометрическую интерпретацию на комплексной плоскости, где вещественная ось соответствует Re, а мнимая ось - Im. Мнимая единица можно представить как точку на плоскости, отстоящую единичное расстояние от начала координат.
6. Cвязь с тригонометрией: Мнимая единица позволяет представить тригонометрические функции (синус, косинус) с использованием экспоненциальной формы. Это полезное свойство, которое позволяет упростить многие вычисления и доказательства.
Таким образом, мнимая единица имеет множество свойств и использование в математике, где она играет важную роль в различных областях, таких как алгебра, геометрия, анализ и физика.
Применение мнимой единицы в математике и физике

Мнимая единица обозначается символом i и задается соотношением i2 = -1. Важно отметить, что мнимая единица не имеет физического смысла и является математическим концептом. Однако, она находит свое применение во многих областях науки, включая математику и физику.
В математике мнимая единица используется для решения уравнений, которые не имеют вещественных корней. Благодаря мнимой единице, можно решать такие уравнения и получать комплексные числа. Комплексные числа имеют важное значение в теории вероятностей, электротехнике, теории сигналов и других областях математики и физики.
В физике мнимая единица также находит широкое применение. Она используется для описания электрических и магнитных полей, колебаний и волновых процессов. Например, в комплексной анализе электромагнитных полей, комплексные числа с мнимыми единицами позволяют легко описывать различные физические явления.
Благодаря использованию мнимой единицы, становится возможным более простое описание сложных физических явлений и их математическое моделирование. Кроме того, мнимая единица позволяет упростить решение сложных задач, таких как расчет электрических цепей или определение сопротивления и емкости в различных системах.



