Медиана треугольника – это линия, которая соединяет вершину треугольника с серединой противоположной стороны. Другими словами, медиана является отрезком, делящим сторону треугольника пополам и проходящим через противоположную вершину. Всего у треугольника три медианы, пересекающиеся в одной точке – центре тяжести.
Вершина треугольника – это одна из трех точек, образующих треугольник. Вершины определяют положение и форму треугольника. Они обозначаются буквами, например, A, B и C. Вершина также может быть назначена в качестве точки отсчета при измерении углов и сторон треугольника.
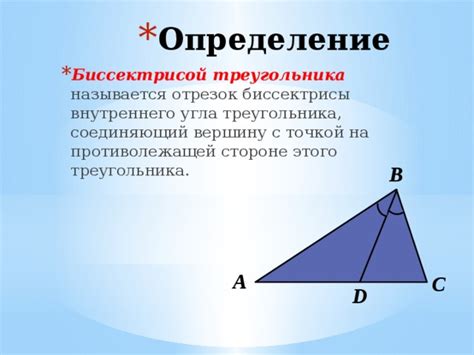
Биссектриса треугольника – это линия, которая делит угол треугольника на две равные части. Биссектриса проходит через вершину угла и делит противоположную сторону на две части, пропорциональные смежным сторонам треугольника. В треугольнике всего три биссектрисы, каждая из которых делит один из трех углов на две равные части.
Медианы, вершины и биссектрисы треугольника являются важными элементами при изучении геометрии. Они помогают нам определить различные свойства и характеристики треугольников и применяются в различных математических задачах и решениях. Понимание этих понятий помогает нам лучше понять и анализировать треугольники и их составляющие части.
Медиана, вершина и биссектриса треугольника
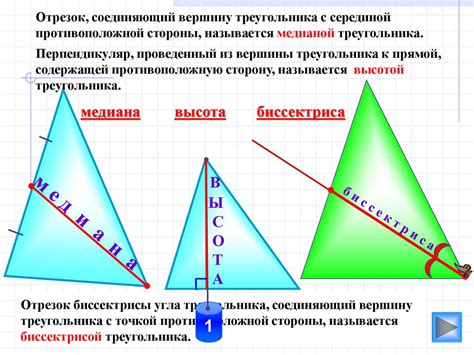
Медиана - это отрезок, соединяющий вершину треугольника с серединой противолежащей ей стороны. В треугольнике каждая из трех сторон имеет свою медиану.
Вершина треугольника - это точка пересечения трех его сторон. Вершина может быть остроугольной, тупоугольной или прямоугольной в зависимости от углов треугольника.
Биссектриса - это отрезок, который соединяет вершину треугольника с точкой на противолежащей ей стороне и делит эту сторону на две равные части. В треугольнике каждый из трех углов имеет свою биссектрису.
Медиана, вершина и биссектриса треугольника играют важную роль в его геометрических свойствах и связях между сторонами и углами треугольника. Они используются при решении задач на построение треугольников и в других областях геометрии.
Определение медианы треугольника
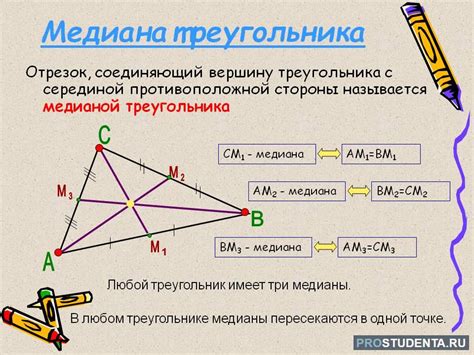
Всякий треугольник имеет три медианы - одну, исходящую из каждой вершины. Медианы треугольника пересекаются в точке, называемой центром тяжести. Это особая точка на плоскости, которая делит каждую медиану в отношении 2:1. Другими словами, медиана, исходящая из вершины, равна полусумме двух сторон, содержащих эту вершину.
Медиана является важным элементом треугольника, так как обладает рядом интересных свойств и применений. Например, медиана делит площадь треугольника на две равные части. Она также служит опорным элементом в конструкции различных геометрических фигур.
Изучение медиан треугольника является важным этапом в геометрии и позволяет лучше понять его структуру и свойства.
Определение вершины треугольника

Вершины треугольника играют важную роль в его определении и характеристиках. Например, через вершины можно провести медианы, биссектрисы и высоты треугольника. Также вершины определяют углы треугольника и позволяют вычислять его площадь и периметр.
Зная координаты вершин треугольника на плоскости, можно определить его форму, тип и свойства. Вершины также могут быть использованы для построения треугольника по заданным условиям или нахождения его центра масс.
Вершины треугольника - это ключевые элементы его структуры и геометрических характеристик, и их правильное определение и использование являются важными при изучении и работе с треугольниками.
Определение биссектрисы треугольника
Для любого треугольника можно провести три биссектрисы, и они пересекаются в одной точке, которая называется центром вписанной окружности. Эта окружность касается всех сторон треугольника.
Биссектрисы треугольника играют важную роль при решении различных задач геометрии. Они используются для нахождения высот, центра тяжести, центра описанной окружности и других параметров треугольника.
Чтобы построить биссектрису угла треугольника, необходимо провести линию, которая делит угол на две равные части. Чтобы это сделать, возьмите циркуль и проведите дугу с центром в вершине угла. Затем повторите этот шаг на другой стороне угла. Точка пересечения этих двух дуг будет являться вершиной биссектрисы. Продолжите линию через эту точку до пересечения с противоположной стороной треугольника.



