Математическая модель - это основа математического анализа и решения разных задач. В 5 классе по программе Петерсона ученики знакомятся с понятием математической модели и учатся применять ее для решения задач различной сложности.
Математическая модель, согласно учебнику Петерсона, представляет собой абстрактную конструкцию, которая описывает реальное явление или процесс. В основе модели лежит математическое выражение или уравнение, которое отражает связи и зависимости между переменными.
Математическая модель может быть представлена в виде графика, таблицы или формулы. Она позволяет учащимся анализировать и предсказывать результаты различных ситуаций, решать задачи и принимать обоснованные решения.
Учение о математических моделях в 5 классе Петерсона помогает развивать логическое мышление и математическую интуицию учеников. Оно позволяет им видеть связь между математикой и реальным миром, а также применять полученные знания в повседневной жизни.
Что такое математическая модель

Математические модели используются в различных областях науки и техники, таких как физика, химия, экономика, биология и др. Например, в физике математические модели используются для описания движения тел, в экономике – для прогнозирования цен и спроса, в биологии – для изучения популяционных динамик и эволюции.
В школьной программе математические модели часто используются для понимания математических понятий и решения задач. Они помогают учащимся увидеть взаимосвязь между математикой и реальным миром, а также развивают абстрактное мышление и логическое мышление.
Определение математической модели

Математическая модель создается на основе определенных предположений и упрощений, которые позволяют описать основные свойства и характеристики изучаемого объекта. Модель может быть представлена в виде схемы, графика, уравнений или таблицы данных.
Математическая модель позволяет проводить различные эксперименты и исследования, предсказывать поведение объекта в различных условиях и оценивать возможные результаты. Она может использоваться в различных областях, таких как физика, экономика, биология, социология и техника.
В школьном курсе математики, изучение математических моделей помогает развить абстрактное и логическое мышление, умение анализировать и решать сложные задачи. Это позволяет учащимся лучше понять законы и принципы функционирования окружающего мира и применять полученные знания на практике.
Применение математической модели

В географии математические модели используются для изучения и прогнозирования различных географических процессов, таких как изменение климата, распределение растительности или миграция животных. Математические модели позволяют учитывать множество факторов и взаимосвязей, которые влияют на эти процессы, и прогнозировать их развитие в будущем.
В экономике математические модели используются для анализа рынков, определения оптимальных стратегий инвестирования, прогнозирования экономического роста и многих других задач. Математические модели позволяют экономистам учитывать различные факторы влияния, такие как предложение и спрос, инфляция и безработица, и прогнозировать развитие экономики.
В медицине и биологии математические модели используются для изучения различных биологических процессов, таких как распространение инфекций, рост популяций или функционирование генетических систем. Математические модели позволяют лучше понимать эти процессы и оптимизировать лечение и превентивные меры.
В физике математические модели используются для описания различных физических явлений, таких как движение тел, распространение волн или реакции веществ. Математические модели позволяют установить законы, которыми следуют эти явления, и предсказать их поведение в различных условиях.
В общем, математические модели играют важную роль в науке и позволяют ученым анализировать сложные процессы, делать прогнозы и находить решения на основе математической логики и методов. Они являются мощным инструментом для понимания и управления миром вокруг нас.
Классификация математических моделей
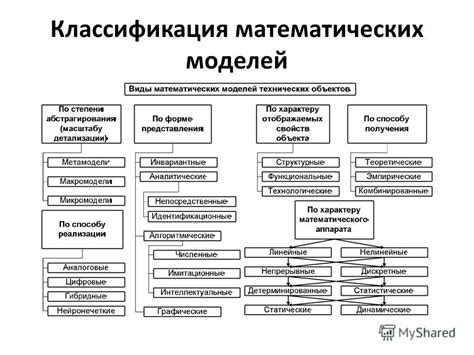
Математические модели могут быть разделены на несколько классов в зависимости от характера задачи, которую они описывают. Вот некоторые из основных классов математических моделей:
| Класс модели | Описание | Примеры |
|---|---|---|
| Физическая модель | Описывает поведение объекта в физическом мире, учитывая его физические свойства и взаимодействие с окружающей средой. | Модель движения тела под действием гравитации |
| Стохастическая модель | Учитывает случайность в системе и предсказывает вероятности различных событий. | Модель марковского процесса |
| Оптимизационная модель | Ищет оптимальное решение задачи, опираясь на определенные критерии или ограничения. | Модель маршрутизации транспортной сети |
| Эмпирическая модель | Основана на экспериментальных данных и позволяет предсказывать результаты на основе наблюдений. | Модель роста популяции |
| Аналитическая модель | Имеет аналитическое решение и представляет собой математическую формулу или уравнение. | Модель распространения тепла |
Классификация математических моделей позволяет ученым и исследователям систематизировать различные подходы и методы, используемые при создании моделей. Это помогает более эффективно решать разнообразные задачи и прогнозировать поведение реальных объектов и систем.
Математическая модель в 5 классе

В 5 классе учащиеся начинают знакомиться с основами математического моделирования. Они учатся создавать простые модели для описания различных ситуаций и задач.
Математические модели позволяют абстрагироваться от реальности и увидеть главное: связи и закономерности между объектами или явлениями. Они помогают ученикам лучше понимать различные математические концепции и применять их на практике.
В процессе создания математической модели ученики могут использовать различные математические операции, формулы и соотношения. Они могут представлять модель с помощью графиков, таблиц, диаграмм и других графических средств.
Примерами математической модели в 5 классе могут служить модель распределения животных в экосистеме, модель роста растения или модель перемещения объекта по прямой.
Важно понимать, что математическая модель - это всего лишь упрощенное представление реальности. Она может не учитывать некоторые факторы или быть ограничена определенными условиями. Поэтому при решении задач с использованием математических моделей необходимо учитывать их ограничения и контекст.
Развитие навыков математического моделирования в 5 классе является важной частью математического образования. Оно помогает ученикам развивать логическое мышление, аналитические навыки и способность применять математические знания на практике.
Методика использования математической модели Петерсона

Процесс использования математической модели Петерсона включает несколько шагов:
- Определение задачи. Сначала необходимо ясно сформулировать задачу, которую необходимо решить с помощью математической модели.
- Выбор переменных. Далее необходимо определить переменные, которые будут использоваться в математической модели. Это могут быть числа, символы или другие элементы.
- Создание таблицы. После определения переменных, следует создать таблицу, в которой будут указаны значения переменных и соответствующие им результаты.
- Анализ данных. Заполните таблицу значениями переменных и вычислите результаты с помощью математической модели. Это поможет вам визуализировать и понять зависимости между переменными.
Методика использования математической модели Петерсона может быть полезна для решения множества математических задач, включая задачи на пропорциональность, решение уравнений, вычисление площадей и объемов и многое другое. Она позволяет структурировать информацию, облегчая процесс решения задачи.
Важно помнить, что правильное понимание и использование математической модели Петерсона требует практики и опыта. Поэтому регулярное практикование и изучение методики играют важную роль в развитии навыков решения математических задач.
Примеры использования математической модели в 5 классе

1. Прогноз погоды: Математические модели позволяют с помощью изучения данных о температуре, давлении, влажности и ветре создать прогноз погоды на основе математических вычислений. Это позволяет предсказывать погоду и принимать соответствующие меры, например, взять зонт или надеть теплую одежду.
2. Моделирование населения животных: С помощью математических моделей можно изучить, как меняется население различных видов животных на основе таких факторов, как биологическая репродукция, естественная смертность и миграция. Это позволяет определить, какие виды находятся под угрозой и принять меры по их сохранению.
3. Моделирование распространения болезни: Математические модели используются для изучения распространения инфекционных заболеваний в обществе. Они могут помочь определить, какие меры необходимы для предотвращения распространения болезни, например, введение вакцинации или карантина.
4. Расчет площади и объема: Математические модели могут использоваться для вычисления площади различных фигур и объема различных тел. Например, с помощью математической модели можно вычислить площадь прямоугольника или объем цилиндра.
В 5 классе использование математической модели позволяет обучающимся применять математику на практике и решать различные жизненные задачи. Это помогает им развивать логическое мышление и аналитические навыки, а также понимать, как математика применяется в реальном мире.



