Координатные точки - это основной инструмент для описания местоположения объектов на координатной оси. В математике координатная ось является одним из ключевых понятий, которое позволяет нам определить положение объекта в пространстве. Координатная ось состоит из двух прямых линий - горизонтальной (ось абсцисс) и вертикальной (ось ординат).
Каждая координатная точка имеет два значения - абсциссу (x-координата) и ординату (y-координата). Абсцисса отображается на горизонтальной оси, а ордината - на вертикальной оси. Таким образом, мы можем определить точное положение объекта в плоскости, используя числовые значения этих координат.
Координатная точка обозначается как (x, y), где x - значение абсциссы, а y - значение ординаты. Например, если у нас есть точка (3, 5), это означает, что данная точка находится на расстоянии 3 единицы от начала горизонтальной оси и на расстоянии 5 единиц от начала вертикальной оси.
Знание координатных точек позволяет нам решать различные математические и геометрические задачи, а также использовать их в различных областях науки и техники. Понимание основных принципов работы с координатными точками открывает перед нами новые возможности и помогает визуализировать различные аспекты пространства и местоположения объектов.
Неизвестные координатные точки на оси
Мы можем указать координату только для тех точек, которые нам известны. Например, на оси мы можем указать координату для точек, представляющих определенные значения величин, таких как время, расстояние или температура. Однако, между этими известными координатными точками находятся бесконечное количество неизвестных точек.
Неизвестные координатные точки на оси могут быть использованы для определения различных свойств и закономерностей математических моделей. Например, мы можем использовать такие точки для определения асимптоты, экстремумов, интервалов возрастания или убывания функции.
Также, неизвестные координатные точки на оси могут быть использованы для построения графиков, диаграмм и других визуальных представлений данных. Мы можем задать диапазон значений оси и расположить на ней точки, представляющие значения определенных параметров.
Важно помнить, что неизвестные координатные точки на оси являются абстракциями и не имеют физического представления в реальном мире. Они существуют только в рамках математических моделей и используются для анализа и представления данных и явлений.
Описание и история

Идея координатной оси восходит к работам античных математиков и астрономов. Греки и Египтяне использовали прямоугольники для измерения площади земли, используя основной принцип координат. Однако формальное определение координатной системы появилось только в XVI-XVII веках благодаря работам математиков Рене Декарта и Пьера Ферма.
Рене Декарт предложил использовать двумерную координатную систему для изучения геометрии. Он предложил поместить две взаимно перпендикулярные горизонтальные и вертикальные линии на плоскости, образуя оси x и y. Точка с координатами (0, 0) была установлена в пересечении этих осей и служила символом начала координат.
Позже в математике был разработан трехмерный аналог координатной системы, добавляющий третью ось z для описания точек в пространстве. С течением времени координатные точки стали все более популярными и широко использовались в различных областях науки и техники.
Как определить координаты
Для определения координат точек на координатной оси необходимо знать два значения: абсциссу и ординату.
Абсцисса определяет положение точки на горизонтальной оси и обозначается числом или буквой, например, "x".
Ордината определяет положение точки на вертикальной оси и также обозначается числом или буквой, например, "y".
Чтобы определить координаты точки на плоскости, необходимо указать значение абсциссы и ординаты точки в порядке (абсцисса, ордината), обычно записываем в виде (x,y).
Например, если точка находится на пересечении горизонтальной оси в точке 3 и вертикальной оси в точке 4, то координаты этой точки будут (3,4).
Зная координаты точки на плоскости, мы можем однозначно определить ее положение и расстояние от начала координат.
Определение координат точек на координатной оси играет важную роль в математике, физике, геометрии и других науках.
Применение координатных точек
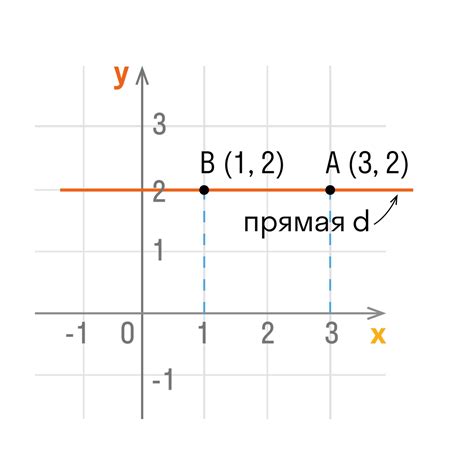
- Математика: координатные точки используются для определения положения объектов на плоскости и решения геометрических задач. Они позволяют вычислять расстояния между точками, находить периметр и площадь фигур, строить графики функций и многое другое.
- Физика: в физике координатные точки позволяют описывать движение объектов и определять их скорость и ускорение. Они необходимы для построения физических моделей и прогнозирования поведения систем.
- География: координатные точки используются для определения местоположения объектов на земной поверхности. С их помощью строятся карты, определяются координаты географических объектов и путей следования.
- Навигация: координатные точки необходимы для определения положения и маршрута объектов во многих сферах деятельности, например, в автомобильной и авиационной навигации.
- Информационные технологии: в программировании координатные точки используются для работы с графикой, создания пользовательских интерфейсов, моделирования и визуализации данных.
Применение координатных точек широко распространено и важно для понимания и анализа многих явлений и процессов в различных областях знания.
Значение в математике

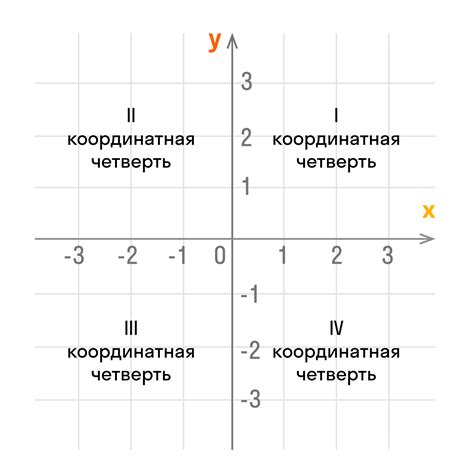
Зная координаты точки, мы можем определить ее положение на плоскости. Если точка имеет положительные координаты по обеим осям, она будет находиться в I квадранте. Если у точки положительное значение x и отрицательное значение y, она будет находиться в IV квадранте. Аналогично, точки с отрицательными значениями x и y будут находиться во II и III квадрантах соответственно.
Координатные точки также используются для определения расстояния между двумя точками на плоскости. Это основа для формулы расстояния между двумя точками, которая вычисляется с использованием теоремы Пифагора.
Использование в географии и навигации

Координатные точки на координатной оси играют важную роль в географии и навигации. Они позволяют определить точное местоположение объекта на Земле и обозначить его на карте или навигационной системе.
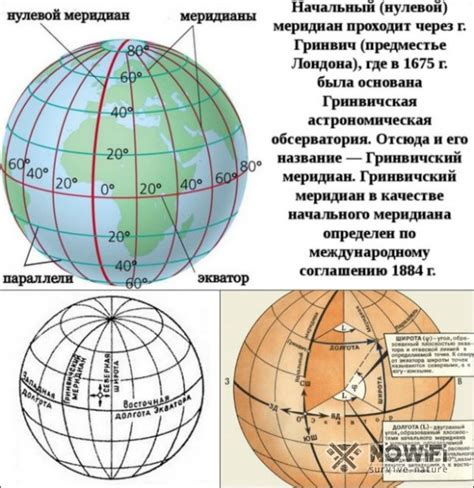
В географии координаты используются для определения географической широты и долготы места. Географическая широта измеряется от экватора до полюсов, а долгота измеряется от Гринвичского меридиана до любого другого места на Земле. Комбинация широты и долготы позволяет однозначно определить местоположение любой точки на земной поверхности.
В навигации координаты используются для определения местоположения судна, самолета или другого транспортного средства. С помощью спутниковой навигационной системы (например, GPS), объекты находят свои координаты и могут планировать маршрут, придерживаться заданного курса и точно указывать своё текущее положение.



