Векторы - это величины, которые имеют не только величину, но и направление. Их широко используют в многих областях, таких как математика, физика и компьютерная графика. Одним из основных понятий, связанных с векторами, является их коллинеарность.
Векторы коллинеарны, если они направлены вдоль одной и той же прямой или параллельны друг другу. То есть, если два вектора можно пропорционально связать между собой. Например, векторы AB и CD являются коллинеарными, если их можно представить как AB = k ⋅ CD, где k - некоторое число.
С другой стороны, неколлинеарные векторы не находятся на одной прямой и не параллельны. Их направления различны. Например, векторы AB и BC являются неколлинеарными, так как их не возможно представить в виде AB = k ⋅ BC.
Различие между коллинеарными и неколлинеарными векторами имеет важное значение при решении задач векторной алгебры. Понимание этого понятия позволяет более точно анализировать и интерпретировать векторные данные. Это также отражается в реальном мире: например, коллинеарные векторы могут представлять движение по одной и той же линии, а неколлинеарные векторы могут представлять движение по разным направлениям.
Коллинеарные векторы: определение и свойства
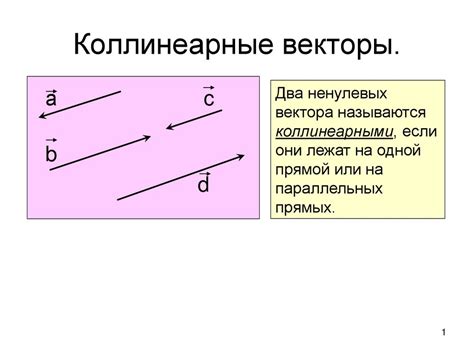
Если существует такое число λ, что векторы a и b могут быть выражены как a = λb, то они считаются коллинеарными. Таким образом, коллинеарные векторы могут быть пропорциональными друг другу.
Свойства коллинеарных векторов:
- Коллинеарные векторы имеют одинаковую или противоположную направленность.
- Они лежат на одной прямой или параллельны друг другу.
- Выполняется равенство a = λb для некоторого числа λ.
- Если a и b коллинеарны, то их длины также пропорциональны, то есть |a| = |λb| = |λ| * |b|.
- Коллинеарные векторы могут быть использованы для построения прямой линии или решения системы уравнений.
Примеры коллинеарных векторов включают параллельные отрезки, направленные в одну и противоположные стороны, радиусы окружности, лежащие на одной прямой, и многие другие примеры из геометрии и физики.
Понятие коллинеарности векторов

Коллинеарные векторы представляют собой векторы, которые лежат на одной прямой или параллельны друг другу. Другими словами, коллинеарные векторы имеют одинаковое направление или противоположные направления.
Для определения коллинеарности векторов можно использовать следующий критерий: если два ненулевых вектора можно представить как произведение одного вектора на число, то они являются коллинеарными.
Примеры коллинеарных векторов:
- Векторы v = (2, 4) и w = (4, 8) являются коллинеарными, так как w = 2v.
- Векторы a = (1, 3) и b = (-2, -6) тоже являются коллинеарными, так как b = -2a.
Коллинеарными могут быть не только два вектора, но и более двух векторов. Важно отметить, что нулевой вектор всегда коллинеарен любому вектору, так как он может быть получен умножением на ноль.
Коллинеарные векторы имеют не только одинаковое направление или противоположное направление, но и могут иметь разные длины. Однако, их отношение остается постоянным.
Свойства коллинеарных векторов

2. Сонаправленность: Коллинеарные векторы направлены в одном и том же направлении или в противоположных направлениях. Если векторы a и b коллинеарны, то они сонаправлены, если k > 0, или противоположно направлены, если k < 0.
3. Лежание на одной прямой: Коллинеарные векторы всегда лежат на одной прямой. Это означает, что они могут быть выражены через линейную комбинацию других векторов, лежащих на этой же прямой.
4. Определение коллинеарности: Для проверки коллинеарности двух векторов a и b, необходимо установить, что отношение их соответствующих координатных компонент пропорционально. То есть, для векторов a = (a1, a2, a3) и b = (b1, b2, b3) существует число k, такое что a1/b1 = a2/b2 = a3/b3.
Знание свойств коллинеарности векторов помогает в решении различных задач в геометрии, физике и других областях науки.
Неколлинеарные векторы: определение и свойства
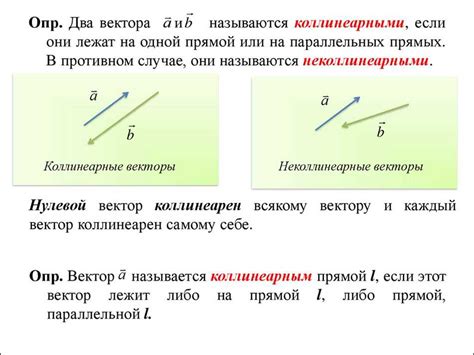
Основное свойство неколлинеарных векторов заключается в том, что они являются линейно независимыми. Это означает, что невозможно выразить один неколлинеарный вектор через другой или их комбинацию с помощью умножения на скаляр.
Неколлинеарные векторы имеют одинаковое направление и могут иметь разную длину. Они могут быть параллельными или скользящим представлением друг друга. К примеру, если два вектора а и b не совпадают друг с другом и не являются коллинеарными, то они неколлинеарны.
Существуют различные методы определения неколлинеарности векторов, такие как проверка условия коллинеарности (если два вектора параллельны или противоположны), анализ определителя матрицы из компонент векторов, метод синусов и другие.
Неколлинеарные векторы играют важную роль в различных областях математики и физики. Например, они используются при решении систем линейных уравнений, в геометрии для построения неколлинеарных треугольников, а также в физике для моделирования движения объектов в пространстве.
Понятие неколлинеарности векторов

В линейной алгебре понятие неколлинеарности векторов играет важную роль. Векторы называются неколлинеарными, если они не лежат на одной прямой. Неколлинеарные векторы имеют разные направления и не могут быть пропорциональными. Также неколлинеарные векторы независимы, что означает, что ни один из них не может быть представлен в виде линейной комбинации других.
Одним из примеров неколлинеарных векторов являются векторы движения. Рассмотрим два вектора: A и B, где A указывает на север, а B указывает на восток. Они имеют разные направления и не лежат на одной прямой, поэтому являются неколлинеарными.
| Вектор | Координаты |
|---|---|
| A | (0, 1) |
| B | (1, 0) |
Другим примером неколлинеарных векторов являются орты X и Y в трехмерном пространстве. Вектор X указывает на ось X, а вектор Y указывает на ось Y. Они не лежат на одной прямой и имеют разные направления, поэтому их можно считать неколлинеарными.
| Вектор | Координаты |
|---|---|
| X | (1, 0, 0) |
| Y | (0, 1, 0) |
Неколлинеарные векторы являются важным концептом в линейной алгебре и находят применение в различных областях, таких как графика, физика и компьютерная графика.
Свойства неколлинеарных векторов

Свойства неколлинеарных векторов включают:
- Независимость: Неколлинеарные векторы линейно независимы, что означает, что ни один из них не может быть выражен в виде линейной комбинации других векторов.
- Ортогональность: Если два неколлинеарных вектора являются ортогональными, то их векторное произведение будет равно нулю.
- Плоскость: Неколлинеарные векторы образуют плоскость, которая проходит через начало координат. Эта плоскость может быть описана как линейное пространство, порожденное этими векторами.
- Масштабируемость: Неколлинеарные векторы могут быть умножены на любое число, и результат будет лежать в той же плоскости.
Неколлинеарные векторы широко используются в различных областях, включая геометрию, физику и компьютерную графику, где они играют важную роль при описании пространственной симуляции и моделирования.
Примеры коллинеарных и неколлинеарных векторов
Пример коллинеарных векторов:
- Вектор A(2, 4) и вектор B(4, 8) имеют одинаковое направление и кратное друг другу. Они лежат на одной прямой и могут быть выражены как A = 2B или B = 0.5A.
- Вектор C(3, -6) и вектор D(-6, 12) имеют противоположные направления, но все равно лежат на одной прямой. Они могут быть выражены как C = -2D или D = -0.5C.
Пример неколлинеарных векторов:
- Вектор E(2, 3) и вектор F(-4, 6) имеют разные направления и не лежат на одной прямой.
- Вектор G(1, 0) и вектор H(0, 1) имеют перпендикулярное направление и также не лежат на одной прямой.
Определение коллинеарности и неколлинеарности векторов важно при решении задач в физике, геометрии и других науках, где требуется анализ векторных величин.



