Иррациональные числа – это числа, которые не могут быть представлены в виде десятичной или обыкновенной дроби. Они отличаются от рациональных чисел, которые могут быть представлены в виде дробей.
Иррациональные числа имеют бесконечное количество десятичных разрядов и не повторяются или не имеют периодической структуры. Из-за этого их запись может быть представлена только с определенной степенью точности.
Примером иррационального числа является пи (π), которое равно отношению длины окружности к ее диаметру. Значение пи приближенно равно 3,1415926535 и далее. Иррациональность числа пи была доказана в древней Греции и до сих пор остается предметом исследований математиков.
Другим примером является корень квадратный из двух (√2), который невозможно представить в виде десятичной дроби. Значение корня из двух приближенно равно 1,4142135623 и далее. Это число было доказано иррациональным в Древней Греции и считается одним из фундаментальных иррациональных чисел.
Что такое иррациональные числа
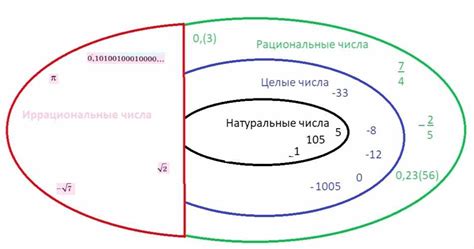
Одним из наиболее известных иррациональных чисел является числовая постоянная π (пи). Она определяется как отношение длины окружности к её диаметру и приближённо равна 3.14159265358979323846... В отличие от рациональных чисел, пи не может быть точно представлено в виде конечной десятичной дроби или периодической десятичной дроби.
Еще одним примером иррационального числа является √2 (квадратный корень из 2). Оно также не может быть представлено в виде дроби и имеет бесконечное количество десятичных знаков без периода.
Иррациональные числа играют важную роль в математике и широко используются в различных научных и инженерных расчетах, а также в других областях, где требуется точное представление чисел и расчеты с высокой точностью.
Свойства иррациональных чисел
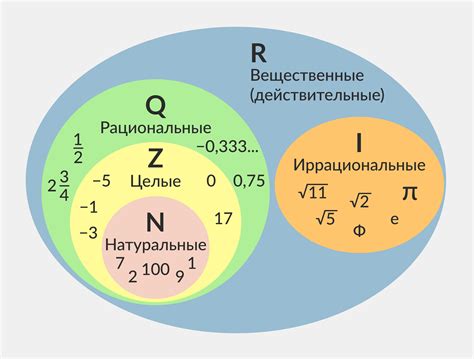
Иррациональные числа обладают рядом интересных свойств, которые делают их особенными в контексте математики.
Первое свойство иррациональных чисел заключается в том, что они не могут быть представлены в виде десятичной дроби или отношения двух целых чисел. Например, число √2 не может быть записано в виде обыкновенной десятичной дроби или отношения двух целых чисел. Это свойство делает иррациональные числа непредсказуемыми и интересными для исследования.
Второе свойство иррациональных чисел заключается в том, что они бесконечны и не периодичны. Это означает, что в их десятичной записи после запятой будет бесконечное количество цифр и никакой периодической последовательности цифр не будет повторяться. Например, число π = 3.14159265358979323846264338327950288419... является иррациональным и его десятичная запись не имеет конца и не повторяется.
Третье свойство иррациональных чисел заключается в их непрерывности на числовой прямой. Иррациональные числа представляют собой бесконечные десятичные дроби, которые между любыми двумя рациональными числами можно найти еще одно иррациональное число. Например, между числами 1.4 и 1.5 можно найти иррациональные числа, например, √2.
Иррациональные числа оказывают важное влияние на различные области математики, физики и других наук. Они являются неотъемлемой частью многих математических теорий и алгоритмов, а также находят применение в компьютерной графике, шифровании информации и других областях.
Примеры иррациональных чисел

| Число | Десятичное представление |
|---|---|
| √2 (квадратный корень из 2) | 1.414213... |
| √3 (квадратный корень из 3) | 1.732050... |
| π (число «пи») | 3.141592... |
| e (число Эйлера) | 2.718281... |
Эти числа являются бесконечными десятичными дробями, которые не имеют повторяющихся или простых закономерностей. Они не могут быть точно представлены в виде рациональных чисел, и их десятичные разложения продолжаются в бесконечность без какого-либо периода или шаблона.
Сравнение иррациональных чисел с рациональными

Иррациональные числа и рациональные числа имеют существенные отличия, и сравнение между ними не всегда тривиально. Рациональные числа могут быть представлены в виде десятичной дроби с конечным или повторяющимся числом знаков после запятой. Иррациональные числа, напротив, не могут быть представлены точно в виде такой дроби или десятичной записи.
Сравнение иррациональных чисел с рациональными может быть выполнено с использованием приближенных значений. Например, пусть есть иррациональное число √2 и рациональное число 1.5. Приближенные значения для этих чисел могут быть вычислены до нужной точности. В данном примере, мы можем вычислить, что приближенное значение для √2 составляет около 1.4142, тогда как приближенное значение для 1.5 равно 1.5.
В результате, мы можем сравнить приближенные значения этих чисел и утверждать, что 1.5 больше, чем √2. Однако, стоит отметить, что это сравнение основано на приближенных значениях и может быть недостаточно точным.
Хотя сравнение между иррациональными числами и рациональными числами может быть неточным, оно по-прежнему полезно и важно для понимания и использования этих чисел в различных научных и математических задачах.
Приближение иррациональных чисел

Например, число π явлется иррациональным числом. Однако, с помощью рациональных чисел, мы можем приблизить его. Например, число 3.14159 является приближением числа π с точностью до пятого знака после запятой. Чем больше знаков после запятой мы учитываем, тем точнее будет приближение иррационального числа.
Другой пример иррационального числа - корень квадратный из 2 (≈ 1.41421). Мы можем приблизить это число с помощью рациональных чисел, например, 1.4 или 1.41, но точное выражение квадратного корня из 2 невозможно.
Иррациональные числа в математике и физике
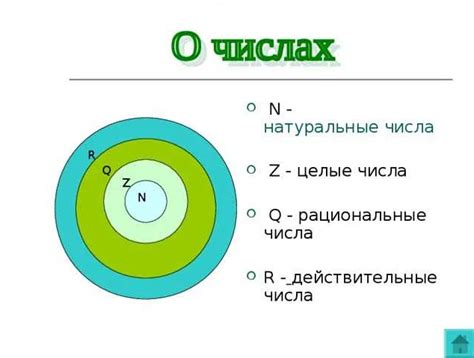
Одним из самых известных примеров иррационального числа является число "пи" (π). Оно определяется как отношение длины окружности к ее диаметру и приближенно равно 3,14159. Однако, число "пи" является бесконечной и непериодической десятичной дробью, что делает его иррациональным. Число "пи" широко используется в математике, физике, инженерии и других науках для вычислений и моделирования объектов, имеющих круговую форму.
Другим примером иррационального числа является "корень из двух" (√2). Оно определяется как положительное число, которое при возведении в квадрат равно двум. Однако, "корень из двух" также является иррациональным числом, так как его десятичное разложение бесконечно и непериодическое. "Корень из двух" также широко используется в математике и физике, особенно в геометрии и алгебре.
Иррациональные числа имеют важные приложения в физике. Например, число "золотого сечения" (φ), которое равно приблизительно 1,61803, является иррациональным числом. Оно широко встречается в природе и используется в искусстве и архитектуре, чтобы создать пропорции, которые считаются эстетически приятными. Одна из самых известных последовательностей, связанных с иррациональными числами, - последовательность Фибоначчи, где каждое число является суммой двух предыдущих чисел, и которая имеет связь с "золотым сечением".
Таким образом, иррациональные числа играют важную роль в математике и физике, позволяя моделировать и анализировать реальные явления и объекты. Они являются фундаментальным инструментом для расширения класса чисел и углубления нашего понимания мира.
Значение иррациональных чисел в практических вычислениях

1. Геометрия: Иррациональные числа часто встречаются в геометрии, особенно при измерении длин сторон и диагоналей. Например, квадратный корень из 2 ( √2) является иррациональным числом и используется для определения длины диагонали квадрата с единичной стороной.
2. Физика: Иррациональные числа применяются в физических вычислениях, особенно в задачах, связанных с волновыми процессами и колебаниями. Например, число π (пи) используется для вычисления длины окружности и площади круга.
3. Алгоритмы и программирование: Иррациональные числа могут быть использованы в алгоритмах и программировании для приближенного расчета функций, которые содержат иррациональные значения. Например, приближенное значение числа e (экспонента) может быть вычислено с использованием ряда Маклорена, который содержит иррациональное число.
4. Финансы: Иррациональные числа также могут иметь применение в финансовых вычислениях. Например, число φ (фи) или золотое сечение, является иррациональным числом и используется в финансовой теории для расчета оптимальных пропорций и отношений.
Иррациональные числа имеют особое значение в практических вычислениях, поскольку они позволяют точнее моделировать и описывать некоторые физические и геометрические явления, а также решать сложные математические задачи. Использование иррациональных чисел в вычислениях помогает получить более точные результаты и более точные модели реального мира.



