Гипербола - одна из основных фигур речи в литературе, широко применяемая при описании и художественном изображении. Гипербола - это усиление выражения, при котором используются преувеличения и преуспешные сравнения.
Одним из примеров использования гиперболы является выражение "смертельно-бледное лицо". Это описание столь бледного лица, что оно выглядит как лицо смертного.
Гиперболические выражения помогают передать сильные эмоции и выделить какое-то явление в тексте. Они создают ощущение перебора или преувеличения, что вносит дополнительную драматичность в произведение. В художественных текстах гипербола может использоваться для экспрессивности и запоминаемости описания и диалогов.
Важно отметить, что гипербола в литературе не всегда является буквальным утверждением, а скорее является образным выражением, допускающим некоторую степень преувеличения. Это делает гиперболу одним из самых ярких и запоминающихся стилистических фигур речи.
Определение и примеры

- Фокусы: точки внутри гиперболы, от которых расстояние до любой точки на кривой равно одному и тому же. Фокусы обозначаются буквами F1 и F2.
- Директрисы: прямые линии, которые проходят через фокусы и перпендикулярны оси симметрии гиперболы.
- Асимптоты: прямые линии, которые находятся бесконечно близко к гиперболе, но никогда не пересекают ее. Они не являются частью гиперболы.
Вот несколько примеров гипербол:
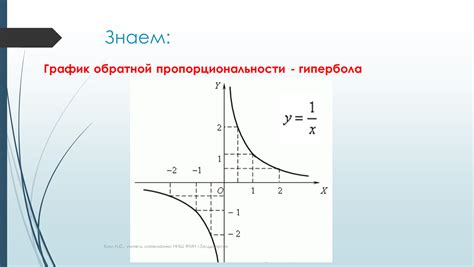
Пример 1: График функции y = 1/x является гиперболой. Ее фокусы находятся в точках (1, 1) и (-1, -1).
Пример 2: График функции y = (x-1)/(x+1) также является гиперболой. Ее фокусы находятся в точках (-1, 0) и (1, 0).
Пример 3: Эллиптическая гипербола – особый тип гиперболы, который имеет центр и фокусы. Она уникальна своим свойством, что сумма расстояний от каждой точки на кривой до фокусов равна постоянной величине.
Структура гиперболы
Структура гиперболы обычно состоит из искусственного увеличения или уменьшения характеристик или качеств предметов или событий. Это может быть выражено через сравнение с чем-то чрезмерным или превратным, или через преувеличение числа или размера.
Гипербола также часто используется для создания комического эффекта или сарказма путем утверждения чего-то очень невероятного или несбыточного. Она может использоваться для усиления эмоциональной нагрузки или для подчеркивания важности чего-то.
В литературе гипербола может использоваться для создания ярких образов, эмоциональной интенсивности и усиления впечатления от произведения. Она может также использоваться для передачи морального или психологического смысла через сильное преувеличение.
Фокусы и директрисы

Фокусы – это точки, которые находятся внутри гиперболы и служат ее основными элементами. Гипербола имеет два фокуса, обозначаемых буквами F1 и F2.
Директрисы – это прямые, которые находятся симметрично относительно оси симметрии гиперболы и служат вспомогательными элементами для ее построения. Гипербола имеет две директрисы, которые обозначаются буквами D1 и D2.
Основное свойство гиперболы заключается в том, что расстояние от каждой точки гиперболы до одного из фокусов минус расстояние до соответствующей директрисы равно постоянной величине. Это свойство называется фокусно-директрисным соотношением и является основой для построения гиперболы.
Фокусы и директрисы играют важную роль при решении задач на построение гиперболы и анализ ее свойств. Знание понятий фокусов и директрис позволяет более глубоко понять и изучить гиперболу и ее особенности.
Основные понятия гиперболы
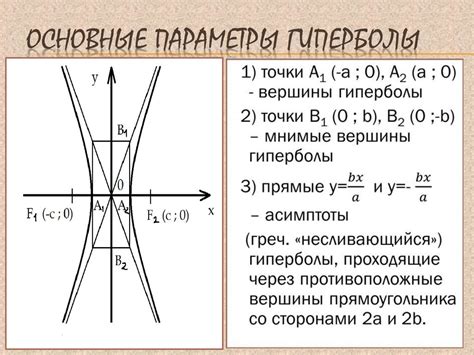
Основные понятия гиперболы:
- Центр гиперболы: точка пересечения осей симметрии - главной оси и побочной оси.
- Фокусы: две точки, расположенные на главной оси и равноудаленные от центра гиперболы. Фокусы обозначаются буквами F1 и F2.
- Директрисы: две прямые, симметрично расположенные относительно центра гиперболы, такие, что любая точка гиперболы находится ближе к одной из директрис, чем к другой. Директрисы обозначаются буквами D1 и D2.
- Расстояние от фокусов до центра: расстояние между центром гиперболы и каждым из фокусов. Обозначается буквой c.
- Основание: отрезок, соединяющий точки пересечения гиперболы с главной осью.
- Расстояние между вершинами: расстояние между точками пересечения ветвей гиперболы. Обозначается буквой a.
- Эксцентриситет: отношение расстояния от фокусов до центра гиперболы к расстоянию между вершинами. Обозначается буквой e.
Знание основных понятий гиперболы помогает в изучении ее свойств и поведения в математических задачах.
Эксцентриситет и центральная ось

Одна из основных характеристик гиперболы – ее эксцентриситет. Эксцентриситет гиперболы обозначается буквой e и определяется как отношение расстояния от центра гиперболы до одной из ее вершин к длине полуоси.
Гипербола также имеет центральную ось – это прямая линия, проходящая через центр гиперболы и перпендикулярная осям симметрии гиперболы. Центральная ось в гиперболе играет важную роль, так как она определяет направление и форму кривой.
Зная эксцентриситет и центральную ось гиперболы, можно определить геометрические свойства и особенности этой кривой. Эти понятия являются основными в изучении и анализе гиперболы и помогают понять ее структуру.
Гипербола в литературе

Гипербола может быть использована как в поэзии, так и в прозе. Она помогает автору выразить свои мысли и чувства более ярко и эмоционально. Гипербола часто используется в различных фигурах, таких как сравнение, метафора и олицетворение, чтобы усилить их эффект.
Примеры гиперболы можно встретить в различных произведениях литературы. В поэзии гипербола позволяет создать мощные образы и эмоциональную атмосферу. Например, в стихотворении Александра Пушкина "Я памятник себе воздвиг нерукотворный" есть строка: "И для разбитых чувств я разлитая слеза" – в этом примере использована гипербола для выражения глубоких эмоций автора.
В прозе гипербола может быть использована для создания комического или драматического эффекта. Например, в романе "Мастер и Маргарита" Михаила Булгакова есть выражение: "Видишь, солнце село!" – в этом примере используется гипербола для подчеркивания удивления и необычности события.
Гипербола – одно из важных средств выразительности в литературе. Она позволяет автору создать эмоциональную связь с читателем и передать свои мысли и чувства с большей силой. Знание гиперболы поможет вам лучше понять и ценить произведения литературы, а также использовать ее в своем собственном творчестве.
Примеры из произведений

| Пример | Произведение | Автор |
|---|---|---|
| Сто раз я тебя предупреждал! | Сказка о рыбаке и рыбке | Александр Сергеевич Пушкин |
| У меня нет ни минуты свободного времени! | Евгений Онегин | Александр Сергеевич Пушкин |
| Ты можешь сделать это миллион раз! | Война и мир | Лев Николаевич Толстой |
Эти выразительные примеры помогают нам лучше понять и запомнить значение гиперболы и насладиться творчеством великих писателей.



