Функция y = 1/x является одной из базовых математических функций и встречается во многих различных областях науки и инженерии. Эта функция описывает зависимость между двумя переменными: x и y, где y обратно пропорциональна x.
Функция y = 1/x имеет график, который является гиперболой в первой и четвертой четверти координатной плоскости. Она имеет вертикальную асимптоту x = 0 и горизонтальную асимптоту y = 0. График функции y = 1/x также симметричен относительно прямой y = x.
Функция y = 1/x широко используется в различных приложениях. Она может быть применена в экономике для моделирования закономерности спроса и предложения, а также в физике для описания обратной зависимости между двумя переменными. Эта функция также использовалась в теории информации для оценки эффективности кодирования и сжатия данных.
Анализ функции y = 1/x
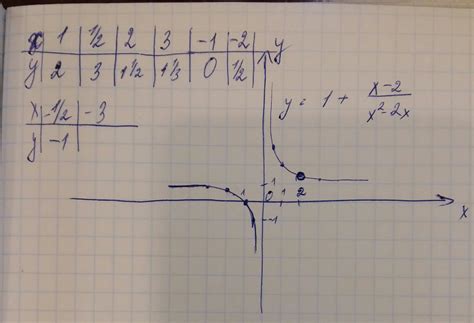
1. Определение области определения: функция y = 1/x определена для всех значений x, кроме x = 0. Это связано с тем, что невозможно поделить на ноль.
2. График: график функции y = 1/x представляет собой гиперболу, проходящую через точку (1, 1) и исключая точку (0, 0). График симметричен относительно оси y = x.
3. Рост и убывание: функция y = 1/x возрастает, когда x убывает, и убывает, когда x возрастает. Это можно увидеть на её графике и подтвердить аналитически.
4. Асимптоты: у функции y = 1/x существуют две асимптоты: вертикальная асимптота x = 0 и горизонтальная асимптота y = 0. График функции стремится к этим асимптотам, но никогда их не пересекает.
5. Значение наилучшей оценки (MVP): наилучшая оценка функции y = 1/x достигается в точке (1, 1), где y = 1. Это значит, что функция имеет минимальное значение в этой точке.
6. Интересные свойства: функция y = 1/x обладает множеством интересных свойств, таких как инверсия, сопряженность и обратимость. Она также является примером обратной функции к линейной функции y = x.
Понятие и определение

Функция y = 1/x определена для всех значений x, кроме нуля, так как деление на ноль невозможно.
График функции y = 1/x представляет собой гиперболу симметричную относительно осей координат.
Функция y = 1/x обладает несколькими важными свойствами:
- Она является убывающей на всей области определения, то есть с увеличением значения x, значение функции уменьшается, и наоборот.
- Она имеет асимптоты y = 0 и x = 0. Приближаясь к нулю по оси абсцисс, значение функции становится бесконечно большим или бесконечно малым.
Функция y = 1/x находит применение в различных областях, включая математику, физику, экономику и другие науки. Она является одной из базовых и фундаментальных функций, которая позволяет описывать различные явления и зависимости между величинами.
График функции y = 1/x
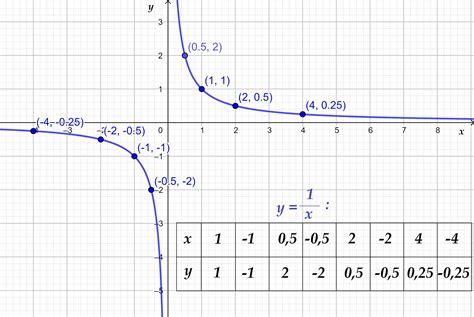
График функции y = 1/x представляет собой гиперболу, проходящую через начало координат (0,0). Форма графика функции зависит от значения аргумента x.
Если x положительно, то y = 1/x будет положительным числом. В этом случае график функции будет расположен в первой и третьей четвертях координатной плоскости. Чем больше значение x, тем ближе значение y к нулю, а график функции приближается к оси y=0 и оси x=0.
Если x отрицательно, то y = 1/x будет отрицательным числом. В этом случае график функции будет расположен во второй и четвертой четвертях координатной плоскости. Также при уменьшении значения x, значение y стремится к нулю.
График функции y = 1/x имеет вертикальную асимптоту y=0 (ось x=0) и горизонтальную асимптоту y=0 (ось y=0).
Различные применения функции y = 1/x
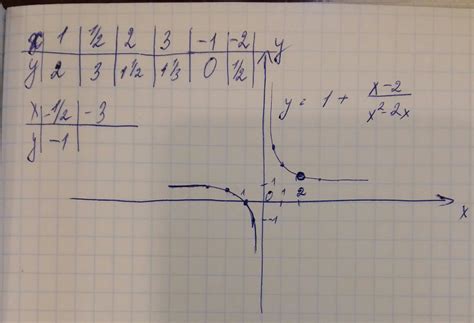
Функция y = 1/x, известная как "обратная функция", имеет множество применений в различных областях науки и техники. Ниже приведены некоторые из них:
- Электротехника: Функция y = 1/x играет важную роль в моделировании различных электрических систем. Например, она может использоваться для описания взаимодействия между сопротивлением и током в электрической цепи.
- Математическая физика: Функция y = 1/x может быть использована для описания явлений, связанных с распределением заряда или массы. Например, она может быть применена для моделирования распределения заряда на проводящем материале или для описания падения силы притяжения между двумя телами с увеличением расстояния между ними.
- Экономика: Функция y = 1/x может использоваться для анализа различных экономических явлений, таких как эластичность предложения или спроса. Например, она может помочь определить, как изменение цены товара влияет на количество продаваемого товара.
- Биология: Функция y = 1/x может быть полезна для описания некоторых биологических процессов. Например, она может использоваться для моделирования зависимости между концентрацией лекарственного препарата в организме и временем после его введения.
Это только несколько примеров, как функция y = 1/x может быть применена в различных областях. Ее уникальные математические свойства делают ее полезной для описания разных явлений и процессов.



