В информатике, особенно в 9 классе, дуга – это один из фундаментальных элементов, используемых в графовых структурах. Графы являются важной частью изучаемых материалов в информатике, так как они позволяют моделировать и анализировать различные сложные системы, включая социальные сети, транспортные сети и многие другие. Дуга представляет собой связь, которая устанавливается между вершинами графа и указывает на то, что между ними существует отношение или взаимодействие.
Дуга в информатике обычно обозначается стрелкой, которая указывает направление связи между вершинами. При этом, дугу можно рассматривать как ориентированную или неориентированную. В случае ориентированной дуги, она имеет однонаправленное направление, показывающее связь от одной вершины к другой. В случае неориентированной дуги, она не имеет направления и указывает, что между вершинами существует двусторонняя связь или взаимодействие.
Дуги в информатике играют важную роль при анализе и обработке графов. Они позволяют представить сложные системы в виде совокупности вершин и связей между ними, что облегчает их изучение и моделирование. Кроме того, дуги могут иметь различные атрибуты и веса, которые позволяют учитывать разные характеристики связей между вершинами. Например, в анализе социальных сетей дуги могут представлять дружеские отношения с разными уровнями интенсивности, что позволяет более точно моделировать социальные взаимодействия.
Дуга в информатике 9 класс

Дуга может быть построена с помощью тега <path> в HTML, который задает путь для перемещения по плоскости. Параметры тега позволяют определить координаты начальной точки, конечной точки и радиус дуги.
Дуга часто используется для создания различных графических объектов, таких как круги, эллипсы и диаграммы. Она может быть использована для отображения связей между различными элементами или для создания эффектов визуализации.
Для создания сложных дуг и кривых можно комбинировать несколько дуг с помощью тега <path>. Также существует возможность задания параметров для управления стилем и цветом дуги.
| Параметр | Описание |
|---|---|
| stroke | Определяет цвет границы дуги |
| stroke-width | Определяет толщину границы дуги |
| fill | Определяет цвет заливки внутри дуги |
Дуги могут быть использованы для создания интерактивных элементов на веб-страницах, таких как кнопки и ссылки. С помощью JavaScript можно добавить действия при нажатии или наведении курсора на дугу.
Значение дуги в информатике
Значение дуги в информатике заключается в том, что она позволяет моделировать различные отношения между объектами или явлениями. Например, в социальных сетях дуги могут представлять дружеские связи между людьми, а в дорожных сетях - дороги, соединяющие города или населенные пункты.
Каждая дуга в информатике может иметь свои характеристики, такие как вес или пропускная способность. Вес дуги характеризует стоимость или длину пути между вершинами, а пропускная способность - скорость передачи информации по данной дуге. Эти характеристики позволяют находить оптимальные пути в графе или решать другие задачи, связанные с передачей данных.
Значение дуги в информатике также проявляется в использовании алгоритмов, разработанных для работы с графами. Например, алгоритм Дейкстры позволяет найти кратчайший путь между двумя вершинами во взвешенном графе, а алгоритм Форда-Фалкерсона - найти максимальный поток в сети с заданными весами дуг.
Таким образом, дуги играют важную роль в информатике, позволяя моделировать и анализировать различные явления с помощью графов. Знание понятия дуги и умение работать с ней является важной компетенцией для программистов и специалистов в области информационных технологий.
Примеры использования дуги в информатике
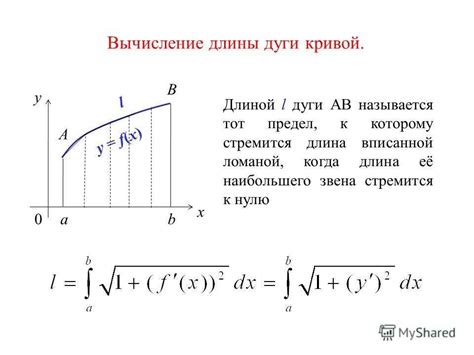
Вот некоторые примеры использования дуги в информатике:
1. Построение ориентированных графов:
Дуги используются для описания связей между объектами или сущностями в различных задачах, таких как моделирование социальных сетей или робототехники. Например, в моделировании соцсетей дуги могут представлять дружеские связи между пользователями, указывая на направление связи от одного пользователя к другому.
2. Навигация в графах:
В алгоритмах на основе графов, дуги используются для определения возможных путей между вершинами графа. Например, в поисковых алгоритмах, таких как алгоритм Дейкстры или алгоритм А* (A-star), дуги используются для определения пути с минимальной стоимостью от начальной вершины к целевой вершине.
3. Маршрутизация в компьютерных сетях:
В компьютерных сетях, дуги могут быть использованы для описания маршрутов передачи данных между устройствами. Например, в протоколе маршрутизации OSPF (Open Shortest Path First), дуги используются для определения оптимальных путей передачи данных в сети.
Таким образом, дуга является важным понятием в информатике и находит широкое применение в различных областях, связанных с графовой теорией и алгоритмами.
Создание дуги в программировании

Дуга в программировании представляет собой графический элемент, который может быть использован для визуализации различных данных или для создания анимации.
Для создания дуги в программировании можно использовать различные языки и технологии, такие как JavaScript, HTML5 и CSS. В HTML5 и CSS есть возможность использовать элемент <svg>, который позволяет создавать графические элементы, включая дуги.
Чтобы создать дугу с использованием <svg>, необходимо задать ее свойства, такие как радиус, начальный и конечный углы и цвет. Например, следующий код создаст дугу с радиусом 50 пикселей, начиная с угла 0 и заканчивая углом 180:
- <svg width="100" height="100">
- <path d="M50 0 A50 50 0 0 0 100 50" fill="none" stroke="black" />
- </svg>
Это пример простой дуги, которая может быть изменена или дополнена в зависимости от требований проекта или задачи. С помощью CSS можно изменять цвет, толщину линии и другие атрибуты дуги.
Создание и использование дуг в программировании может быть полезным для визуализации данных или создания интерактивных элементов на веб-страницах или мобильных приложениях. Это мощный инструмент, который помогает разработчикам создавать более привлекательные и функциональные пользовательские интерфейсы.
Как работает дуга в информатике
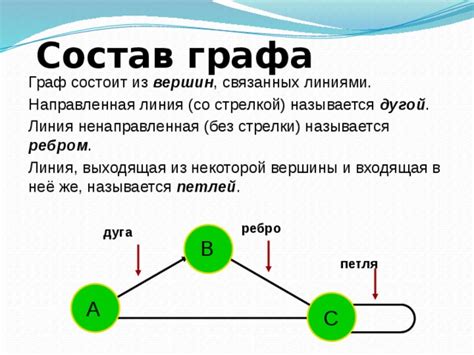
Дуга может быть направленной или ненаправленной. В направленной дуге есть стрелка, указывающая направление движения от одной вершины к другой. Направление указывает на связь между вершинами, где одна вершина является начальной, а другая – конечной. Ненаправленная дуга не имеет стрелки и показывает двустороннюю связь между вершинами.
Дуги могут использоваться в различных алгоритмах, таких как поиск кратчайшего пути в графе или проверка связности вершин. Они помогают визуализировать отношения между объектами и организовывать информацию в структурированном виде.
Дуги часто представляются в виде линий, стрелок или кривых на графическом интерфейсе пользователя. В программировании существуют различные способы представления и работы с дугами в разных языках программирования и библиотеках.
Как правило, дуги в графе хранятся в виде списка или матрицы смежности, где каждая ячейка списка или матрицы указывает на наличие или отсутствие дуги между соответствующими вершинами. Это позволяет эффективно обрабатывать и поисковые операции с графом.
В целом, понимание работы дуг в информатике важно для понимания графовых алгоритмов и структур данных, которые широко применяются в различных областях, включая сетевое программирование, анализ данных и машинное обучение.
Основные свойства дуги в информатике

Основные свойства дуги в информатике:
1. Ориентированность: Дуга может быть ориентированной или неориентированной. Если дуга ориентированная, то она имеет начало и конец, и направление движения. Если дуга неориентированная, то она имеет только начало и конец, без определенного направления.
2. Множество вершин: Дуга может быть связана с одной или более вершинами графа. Вершины, связанные с дугой, называются концами дуги.
3. Вес: Дуга может иметь вес или быть невзвешенной. Вес дуги - это дополнительная информация, которая может быть связана с дугой, например, для указания стоимости перехода от одной вершины к другой.
4. Мультидуги: В некоторых случаях может возникать необходимость в нескольких дугах между двумя вершинами графа. Такие дуги называются мультидугами и используются для представления возможности множественных связей между вершинами.
Дуги являются важной частью графовой теории и широко используются в различных областях информатики, включая алгоритмы, сети, базы данных и другие.
Проектирование дуги в программе

Для создания дуги в программе может использоваться различное программное обеспечение: графические редакторы, компьютерные CAD-системы, программы для разработки игр и другие. При проектировании дуги необходимо указать ее радиус, угол начала и конца, а также координаты центра окружности, на которой она расположена.
Для настройки внешнего вида дуги часто предоставляются дополнительные возможности. Например, можно изменить толщину линии, цвет или стиль отрисовки. Некоторые программы позволяют также добавить текст или изображение внутри дуги, что может быть полезно при создании диаграмм или иллюстраций.
Отдельно стоит отметить возможность анимации дуги. Это означает, что ее параметры – радиус, углы начала и конца – можно изменять во времени, что создает эффект движения. Эта функция широко используется в различных программных приложениях, играх и веб-разработке.
Проектирование дуги в программе требует внимательности и точности, так как от правильности настройки зависит ее внешний вид и функциональность. Однако, овладев навыками работы с графическими элементами, можно создавать красивые и эффективные визуальные эффекты и пользовательские интерфейсы.
Использование дуги в алгоритмах
Использование дуги в алгоритмах представляет ряд преимуществ. Во-первых, дуги позволяют определить направление обхода графа. Это особенно полезно при использовании алгоритмов обхода, таких как алгоритм поиска в ширину или алгоритм Дейкстры. Дуги также позволяют определить направление обработки данных, что может быть полезно при работе с ориентированными графами.
Во-вторых, дуги могут содержать дополнительную информацию о связях между вершинами. Эта информация может быть использована при решении различных задач. Например, в алгоритмах поиска кратчайшего пути, вес дуги может быть использован для определения наименьшего пути между двумя вершинами.
Также дуги могут быть использованы для представления ориентированных связей между объектами в различных предметных областях. Например, в компьютерной графике, дуги могут быть использованы для определения пути движения объекта или для задания направления векторов.
В итоге, использование дуги в алгоритмах предоставляет мощный инструмент для обработки графов и сетей. Он позволяет определить направление обхода, содержит дополнительную информацию о связях между элементами и может быть использован для представления ориентированных связей. Понимание и умение использовать дуги - важные навыки для успешной работы с алгоритмами в информатике.



