Дельта - это математический термин, который означает изменение или разницу между двумя значениями, обозначаемыми символом "Δ" (дельта). Она используется в различных областях, таких как физика, математика и инженерия, для измерения изменений и определения разницы между объектами или значениями.
Найти дельту - это значит вычислить разницу или изменение между двумя значениями. Это может быть полезным, например, для определения скорости, величины или направления изменения. Для вычисления дельты необходимо иметь два значения, между которыми ищется разница.
Существует несколько способов вычисления дельты, в зависимости от того, с какими данными вы работаете. В некоторых случаях достаточно вычесть одно значение из другого, чтобы получить разницу. В других случаях может понадобиться использование специальных формул или уравнений. В любом случае, понимание того, что такое дельта и как ее найти, является важным для многих научных и технических областей.
Как найти дельту в математике
Для нахождения дельты (Δ) нужно знать начальное значение (A) и конечное значение (B). Для двух чисел дельта может быть найдена следующим образом:
| Переменная | Значение |
|---|---|
| Начальное значение (A) | A |
| Конечное значение (B) | B |
| Дельта (Δ) | Δ = B - A |
Например, если у нас есть начальное значение A = 5 и конечное значение B = 10, мы можем найти дельту следующим образом:
Δ = 10 - 5 = 5
Таким образом, дельта в данном случае равна 5.
Дельта также может быть использована для обозначения изменений других величин. Например, если у нас есть начальная температура T1 и конечная температура T2, мы можем найти изменение температуры, используя формулу:
ΔT = T2 - T1
Таким образом, дельта T (ΔT) будет представлять разницу между T2 и T1.
Итак, дельта (Δ) используется для обозначения разности или изменения значений и вычисляется путем вычитания начального значения из конечного значения.
Что такое дельта и как она используется

В математике дельта может быть использована для обозначения разности между двумя числами. Например, если у нас есть два числа - 5 и 3, то разность между ними будет равна 2. Мы можем записать это как "delta = 5 - 3" или "delta = 2".
В физике дельта может использоваться для обозначения изменения состояния системы. Например, если мы измеряем изменение температуры воздуха с течением времени, мы можем использовать символ дельты для обозначения этого изменения. Так, если температура воздуха увеличивается на 2 градуса, мы можем записать это как "delta T = 2".
В информатике дельта может быть использована для обозначения изменения значения переменной. Например, если у нас есть переменная "x", и мы хотим увеличить ее значение на 3, мы можем записать это как "x = x + delta", где "delta" может быть равна 3.
В финансовой сфере дельта относится к изменению стоимости опциона, в зависимости от изменения цены базового актива. Это показатель грека, который используется для измерения риска и волатильности в финансовых рынках.
Таким образом, дельта - это важный инструмент, который используется для измерения изменений и разностей в различных областях. Он помогает нам анализировать и понимать процессы и явления, происходящие вокруг нас.
Формула для нахождения дельты
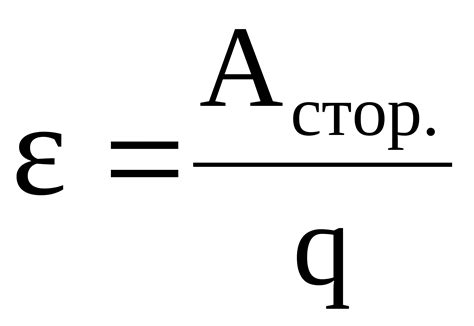
Формула для нахождения дельты в квадратном уравнении выглядит следующим образом:
- Если уравнение имеет вид: ax^2 + bx + c = 0,
- То дельта (Δ) вычисляется по формуле: Δ = b^2 - 4ac.
Здесь:
- a - коэффициент при x^2,
- b - коэффициент при x,
- c - свободный член.
Зная значение дельты (Δ), можно определить количество и тип корней квадратного уравнения. Рассмотрим возможные случаи:
- Если Δ > 0, то уравнение имеет два различных корня.
- Если Δ = 0, то уравнение имеет один корень, которые является двукратным.
- Если Δ < 0, то уравнение не имеет действительных корней.
Теперь, зная формулу для нахождения дельты, вы можете легко определить ее значение и использовать для решения квадратных уравнений.
Пример применения нахождения дельты

Рассмотрим квадратное уравнение вида ax^2 + bx + c = 0, где a, b и c - коэффициенты, а x - неизвестная. При наличии дискриминанта, который является выражением под корнем в формуле нахождения дельты, мы можем определить, сколько корней имеет уравнение и каковы их характеристики.
Если дельта больше нуля, то уравнение имеет два различных корня: x1 и x2. Если дельта равна нулю, то уравнение имеет один корень x. И если дельта меньше нуля, то уравнение не имеет действительных корней.
Пример применения нахождения дельты в решении квадратного уравнения:
function findRoots(a, b, c) {
let delta = b * b - 4 * a * c;
let x1, x2;
if (delta > 0) {
x1 = (-b + Math.sqrt(delta)) / (2 * a);
x2 = (-b - Math.sqrt(delta)) / (2 * a);
} else if (delta === 0) {
x1 = x2 = -b / (2 * a);
} else {
console.log("Уравнение не имеет действительных корней");
return;
}
console.log("Первый корень: " + x1);
console.log("Второй корень: " + x2);
}
findRoots(1, -3, 2);
Таким образом, нахождение дельты позволяет эффективно решать квадратные уравнения и определять их корни.
Какие значения дельты могут быть

Значение дельты может быть положительным, отрицательным или равным нулю в зависимости от результата вычисления разности двух чисел.
Если значение дельты положительное, это означает, что первое число больше второго. Например, если разность равна 5, то первое число на 5 больше второго.
Если значение дельты отрицательное, это означает, что первое число меньше второго. Например, если разность равна -4, то первое число на 4 меньше второго.
Если значение дельты равно нулю, это означает, что два числа равны друг другу. Например, если разность равна 0, то первое число и второе число равны между собой.
Значение дельты является важным показателем при решении различных математических и физических задач. Оно позволяет определить положение и относительную величину различных величин или явлений.



