Матрица - это основной математический объект, который используется в линейной алгебре для представления данных в виде таблицы. Она состоит из элементов, расположенных в ячейках по строкам и столбцам. Матрицы широко применяются в различных областях науки и техники, включая экономику, физику, компьютерную графику и машинное обучение.
Матрицу можно представить как набор строк и столбцов. Строка матрицы состоит из элементов, разделенных пробелами и расположенных один за другим горизонтально. Столбец матрицы представляет собой набор элементов, указанных вертикально. Элементы в строке или столбце матрицы могут быть числами, символами или другими объектами, в зависимости от контекста задачи.
Например, рассмотрим следующую матрицу:
3 1 4
1 5 9
2 6 5
Здесь таблица имеет три строки и три столбца. В первой строке находятся элементы 3, 1 и 4, во второй строке - 1, 5 и 9, а в третьей строке - 2, 6 и 5. Такая матрица может использоваться, например, для представления данных о различных измерениях объекта или для решения системы линейных уравнений.
Матрица строка и столбец: определение и примеры

Матрицей называется прямоугольная таблица чисел или других элементов, расположенных в строках и столбцах. В матрице элементы обычно записываются в квадратные скобки или между вертикальными чертами.
Матрица строка представляет собой матрицу, содержащую только одну строку. То есть, она имеет одну строчку и произвольное количество стобцов. Для обозначения матрицы строка используются заглавные буквы. Например, матрица строка A может выглядеть следующим образом:
A = [1, 2, 3, 4]
Элементы матрицы строка могут быть числами, буквами или другими символами. Они располагаются в одной строке, разделяясь запятыми.
Матрица столбец, напротив, представляет собой матрицу, содержащую только один столбец. То есть, она имеет один столбец и произвольное количество строк. Для обозначения матрицы столбец используются заглавные буквы с индексом нижними буквами. Например, матрица столбец B может выглядеть следующим образом:
B =
[1]
[2]
[3]
[4]
Матрицы строка и столбец могут быть удобными при решении линейных уравнений, систем линейных уравнений и других задач линейной алгебры. Они могут быть использованы при работе с векторами и в обработке данных. Также они могут быть представлены как составные части более сложных матриц.
Определение матрицы
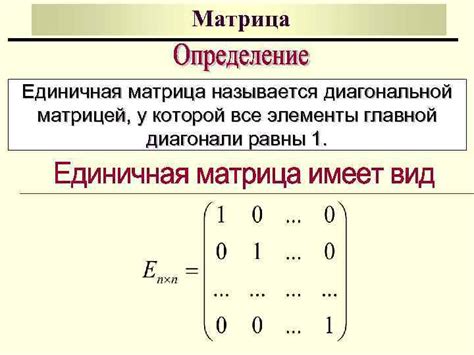
Строки матрицы располагаются горизонтально, а столбцы - вертикально. Каждый элемент матрицы находится в определенной позиции, которая определяется его номером строки и столбца.
Для определения матрицы используется общий формат:
А = [aij]
где A - матрица, aij - элемент матрицы расположенный в i-й строке и j-м столбце.
Например, матрица A размером 2x3 имеет следующий вид:
A =
| a11 | a12 | a13 |
| a21 | a22 | a23 |
Такая матрица состоит из двух строк и трех столбцов, и содержит шесть элементов.
Строки и столбцы в матрице

Строки в матрице представляют собой элементы, расположенные горизонтально. Каждая строка имеет свой номер, указывающий на положение строки относительно остальных. Например, в матрице размером 3x3 первая строка будет иметь номер 1, вторая - номер 2 и так далее.
Столбцы в матрице представляют собой элементы, расположенные вертикально. Каждый столбец также имеет свой номер, указывающий на положение столбца относительно остальных. В матрице размером 3x3 первый столбец будет иметь номер 1, второй - номер 2 и так далее.
Строки и столбцы в матрице удобно использовать для обращения к конкретным элементам. Например, чтобы обратиться к элементу, находящемуся в третьей строке и втором столбце, нужно указать номер строки и номер столбца: [3, 2].
Строки и столбцы играют важную роль в операциях над матрицами. Например, при сложении матриц необходимо складывать соответствующие элементы строк и столбцов. А при умножении матриц используется комбинация строк первой матрицы и столбцов второй матрицы.
Таким образом, понимание строения матрицы с учетом строк и столбцов позволяет лучше понять ее структуру, а также проводить различные операции с данными, связанными с матрицами. Это основа для решения множества задач в математике, программировании, физике и других областях.
Примеры матриц строка и столбец

Пример матрицы-строки:
Матрица-строка представляет собой матрицу, состоящую из одной строки. Например, рассмотрим следующую матрицу-строку:
[2, 4, 6, 8]
В данном примере мы имеем матрицу-строку, состоящую из четырех элементов: 2, 4, 6 и 8. Каждый элемент располагается в одной строке, что является отличительной особенностью матриц-строк.
Пример матрицы-столбца:
Матрица-столбец представляет собой матрицу, состоящую из одного столбца. Рассмотрим следующий пример матрицы-столбца:
[1]
[3]
[5]
В данном примере мы имеем матрицу-столбец, состоящую из трех элементов: 1, 3 и 5. Каждый элемент располагается в отдельном столбце, что является характерной особенностью матриц-столбцов.
Матрицы строка и столбец широко используются в различных областях науки и техники, таких как математика, физика, компьютерная графика и много других. Они являются важными инструментами для работы с данными и решения различных задач.
Операции с матрицами

- Сложение и вычитание: для того чтобы сложить или вычесть две матрицы, нужно их размеры совпадали. Сложение (вычитание) происходит покомпонентно, то есть каждый элемент результирующей матрицы получается как сумма (разность) соответствующих элементов из исходных матриц.
- Умножение на скаляр: умножение матрицы на скаляр означает умножение каждого элемента матрицы на заданное число. Размеры матрицы при этом не меняются.
- Умножение матриц: умножение двух матриц определено, если число столбцов первой матрицы равно числу строк второй матрицы. Результирующая матрица имеет размерность, где число строк равно числу строк первой матрицы, а число столбцов - числу столбцов второй матрицы. Каждый элемент результирующей матрицы вычисляется путем умножения элементов соответствующей строки первой матрицы на элементы соответствующего столбца второй матрицы и их последующего сложения.
- Транспонирование: при транспонировании матрицы строки становятся столбцами, а столбцы - строками. То есть элементы, находившиеся на позиции (i, j) в исходной матрице, переносятся на позицию (j, i) в транспонированной матрице.
Операции с матрицами позволяют решать различного рода задачи, например, находить решения систем линейных уравнений, находить собственные значения и векторы матрицы, выполнять преобразования координат в геометрии и многое другое.
Применение матриц строка и столбец

Матрицы строка и столбец играют важную роль в различных областях науки, техники и информатики. Они широко применяются для представления данных и решения различных задач.
Одно из основных применений матриц строка и столбец - это работа с линейными уравнениями и системами уравнений. Например, системы уравнений могут быть представлены в виде матрицы, где каждая строка соответствует уравнению, а каждый столбец - переменным. Путем алгебраических операций с матрицами можно решить такие системы и найти значения неизвестных.
Матрицы строка и столбец также используются в компьютерной графике для преобразования и отображения объектов. Например, в трехмерной графике матрица 4x4, содержащая значения координат, поворотов и масштабирования, применяется для трансформации трехмерных моделей и преобразования их видимости на экране.
Еще одним применением матриц строка и столбец является обработка и анализ изображений. Матрицы могут использоваться для фильтрации изображения, изменения его яркости и контрастности, а также для обнаружения особых узоров и объектов.
Матрицы строка и столбец также находят применение в статистике и экономике. С помощью матриц можно анализировать данные, вычислять статистические показатели, строить модели и прогнозировать результаты.
Таким образом, матрицы строка и столбец имеют широкий спектр применений и являются важным инструментом для работы с данными и решения различных задач.



