Смешанное число - это число, которое состоит из целой части и дробной части. В математике смешанное число используется для представления чисел, которые больше единицы, но меньше двух, и имеют десятичную часть, которая не равна нулю.
Смешанное число можно представить в виде суммы целого числа и дроби. Обычно смешанное число записывается в виде целой части, за которой следует дробь, например 1 2/3 или 3 1/4. Целая часть числа позволяет определить, сколько полных единиц содержится в смешанном числе, а дробная часть указывает на оставшиеся части единицы.
Смешанные числа часто применяются в реальной жизни, особенно при работе с измерениями или дробными данными. Например, если вы хотите представить длительность времени в часах и минутах, то можете использовать смешанное число. Также смешанные числа могут быть полезны при работе с денежными величинами, долями и многими другими величинами, которые имеют дробную часть и целую часть одновременно.
Определение и понятие

Пусть у нас есть смешанное число, например, 3 1/2. Здесь число 3 - это целая часть, а 1/2 - это дробная часть. Чтобы представить это число как сумму, мы можем записать его как 3 + 1/2.
Смешанное число может быть записано разными способами. Например, 3 1/2 может быть записано как 3,5 или как 7/2. В то же время, 2 3/4 может быть записано как 2,75 или как 11/4. Все эти записи представляют одно и то же число, просто в разных форматов.
Смешанные числа полезны при работе с обыкновенными дробями и в решении различных задач, включая задачи на смешанные числа, десятичные и обыкновенные дроби. Они позволяют нам представить целую часть и дробную часть числа вместе, что упрощает его использование в математических расчетах и операциях.
Операции с смешанными числами включают сложение, вычитание, умножение и деление. Для выполнения этих операций нам нужно представить смешанное число в виде обычной десятичной дроби или обыкновенной дроби. Затем мы можем применить обычные правила арифметики для выполнения операции.
| Смешанное число | Десятичная дробь | Обыкновенная дробь |
|---|---|---|
| 3 1/2 | 3,5 | 7/2 |
| 2 3/4 | 2,75 | 11/4 |
Как записывается смешанное число
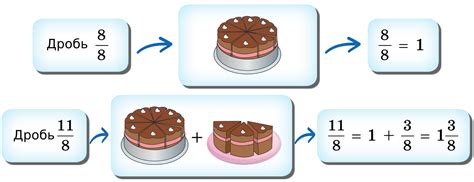
- 3+1/2
- 2+3/4
- 5+2/3
Чтобы записать смешанное число в более компактной форме, используются арифметические знаки. Например:
- 3+1/2 можно записать как 3 1/2
- 2+3/4 можно записать как 2 3/4
- 5+2/3 можно записать как 5 2/3
Запись смешанного числа в виде целой части и дроби позволяет получить более наглядное представление числа и упростить выполнение арифметических операций с ним.
Перевод смешанного числа в десятичную дробь

Смешанное число представляет собой комбинацию целой части и дробной части. Для перевода смешанного числа в десятичную дробь следует выполнить следующие шаги:
1. Умножьте целую часть на знаменатель дроби и прибавьте числитель:
| Смешанное число | Целая часть | Дробная часть |
|---|---|---|
| 3⁄2 | 3 | 1⁄2 |
Умножим 3 на 2 и прибавим 1:
3 * 2 + 1 = 7
2. Разделите полученное число на знаменатель и запишите результат в качестве дробной части:
Для числа 7 и знаменателя 2:
7 ÷ 2 = 3.5
Полученное число 3.5 является десятичной записью смешанного числа 3⁄2.
Примеры использования смешанных чисел

Пример 1:
Представим, что у нас есть карта марафона длиной 42.195 км. Однако, чтобы легче ориентироваться, нам хочется разделить эту дистанцию на целое количество кругов стандартной длины – 10 км. Сколько целых кругов мы сможем пройти и какая будет разница между пройденным пути и полными кругами?
Используя смешанное число, мы можем ответить на этот вопрос. Первая часть числа будет показывать количество полных кругов (натуральное число), а вторая часть – разницу между пройденной дистанцией и полными кругами (дробная часть числа).
В данном случае, количество полных кругов будет равно 4, а разница в пути составит 2.195 км.
Пример 2:
Представьте, что вам нужно купить 7 упаковок сока, а каждая упаковка содержит 0.5 литра. Используя смешанное число, мы можем легко определить, сколько литров сока вам нужно купить.
Первая часть числа будет показывать количество полных упаковок (натуральное число), а вторая часть – разницу между количеством сока в полных упаковках и общим количеством сока (дробная часть числа).
В данном случае, количество полных упаковок будет равно 7, а разница в количестве сока составит 0.5 литра.
Свойства и особенности смешанных чисел

Основные свойства смешанных чисел:
- Смешаные числа могут быть преобразованы в обыкновенные дроби путем сложения целой части с дробной: a b/c = (a * c + b)/c.
- Смешаные числа могут быть преобразованы в десятичные дроби, путем деления числителя на знаменатель и сложения с целой частью.
- Смешаные числа могут быть складывены, вычитаны, умножены и делены так же, как и обыкновенные дроби.
- Смешаные числа могут быть преобразованы в неправильные дроби путем умножения целой части на знаменатель, сложения числителя и знаменателя, и деления на знаменатель: a b/c = (a * c + b)/c.
- Смешаные числа могут быть сравнены путем преобразования их в обыкновенные дроби и сравнения числителей.
Смешаные числа часто используются в повседневной жизни и могут быть полезны при измерении и представлении результатов в различных областях, таких как временные интервалы, измерение длины или объема.
Учебное пособие предоставлено OpenAI API.



