R в математике обозначает числовое множество вещественных чисел, которое включает все рациональные и иррациональные числа. Оно является основной числовой системой, используемой для измерения и описания физических явлений и математических отношений.
Множество R состоит из всех действительных чисел, которые могут быть представлены на числовой оси. Оно включает все целые числа, дроби, а также числа, которые не могут быть представлены в виде конечной или периодической десятичной дроби, такие как корни квадратные и числа π и е.
Область значений R очень широка, и она применяется во множестве областей, включая физику, экономику, статистику, геометрию и многие другие науки. Она позволяет ученым и математикам описывать и анализировать различные явления и взаимодействия в природе и обществе, используя точные и строгие методы расчета и измерения.
Определение R в математике

R (от английского слова "real") в математике обозначает множество всех действительных чисел. Оно включает все рациональные и иррациональные числа. Действительные числа представляют собой числа, которые можно изобразить на числовой прямой, включая как целые числа, так и дроби. Более формально, множество R можно определить как основное числовое поле, в котором выполняются все основные арифметические операции, такие как сложение, вычитание, умножение и деление.
R также включает в себя специальные числа, такие как бесконечность и неопределенности. Бесконечность в R обозначается символом ∞ и представляет числа, которые стремятся к положительной или отрицательной бесконечности. Неопределенность возникает, когда результат арифметической операции не может быть определен точно, например, деление на ноль. Эти специальные числа играют важную роль в математике и науке, и их изучение является частью теории действительных чисел.
R - множество всех вещественных чисел
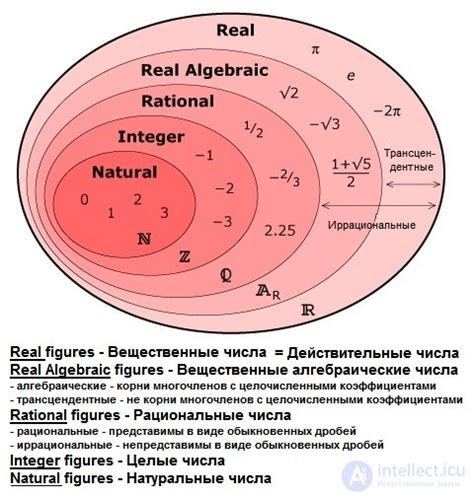
Множество R содержит все числа, которые могут быть представлены в виде десятичной дроби с бесконечным количеством десятичных знаков (например, $\pi$ или $\sqrt{2}$). Оно также содержит все рациональные числа, которые могут быть представлены в виде обыкновенной дроби (например, $\frac{3}{4}$ или $\frac{5}{2}$).
Множество R имеет следующие характеристики:
- Неограниченность: множество R не имеет ни наибольшего, ни наименьшего элемента. Это означает, что можно найти число, большее или меньшее любого заданного числа.
- Плотность: в любом интервале между двумя числами из множества R всегда можно найти другое число (например, между 1 и 2 можно найти 1.5).
- Непрерывность: множество R не имеет пропусков или разрывов, каждое число имеет соседей с обеих сторон.
- Мощность: мощность множества R равна континууму, т.е. оно имеет мощность континуума и больше мощности множества натуральных чисел или множества рациональных чисел.
Множество R широко используется в математике, физике и других науках для описания и изучения непрерывных величин и процессов. Оно является основой для различных математических теорий и моделей, таких как теория вероятностей, дифференциальное исчисление, интегральное исчисление и другие.
Область значений R
Область значений R, или числовая прямая, представляет собой множество всех действительных чисел. R в математике обозначает множество всех чисел, которые могут быть представлены на числовой оси.
Действительные числа включают в себя все целые числа, рациональные числа (которые могут быть записаны как отношение двух целых чисел), а также иррациональные числа (которые не могут быть записаны как отношение двух целых чисел).
R является бесконечной и непрерывной числовой прямой, где каждая точка на оси соответствует уникальному действительному числу. Диапазон значений чисел R неограничен, и он охватывает все возможные числовые значения.
Математические операции, такие как сложение, вычитание, умножение и деление, выполняются с числами в множестве R. R является основной числовой системой, используемой в математике и других науках.
Важно заметить, что область значений R также может быть ограничена в конкретном контексте и задаче. Например, в задачах, связанных с физическими величинами или ограниченным интервалом времени, область значений может быть ограничена определенным диапазоном чисел в R.
R имеет бесконечную область значений

Математическая переменная R обозначает множество всех действительных чисел. Разнообразие чисел, которые могут принимать значения R, не знает ограничений и включает в себя все положительные и отрицательные числа, нуль и бесконечные числа. Такое бесконечное расширение R делает его особенно полезным в математических расчетах и моделях, так как позволяет представлять и решать широкий спектр проблем.
Кроме того, R является линейно упорядоченным множеством, что значит, что любые два числа в R можно сравнивать в отношении их величины. Например, можно сравнивать, является ли одно число больше, меньше или равным другому числу.
Область значений R используется не только в математике, но и во многих других науках и областях знаний. Она является основой для создания математических моделей, решения уравнений, анализа данных и многих других приложений. Благодаря своей бесконечной области значений, R предоставляет нам неограниченные возможности для работы с числами и проведения сложных вычислений.



