Передаточная функция звена или системы является одной из основных концепций в теории управления. Это математическое выражение, которое описывает связь между входным и выходным сигналами системы. Путем анализа передаточной функции можно получить информацию о поведении системы в зависимости от различных входных сигналов.
Передаточная функция обычно представляется в виде дробно-рациональной функции, где числитель и знаменатель содержат коэффициенты, представляющие параметры системы. Числитель представляет влияние входного сигнала на выход, а знаменатель - влияние шумов и помех на систему. Анализируя передаточную функцию, можно определить устойчивость, точность и скорость реакции системы на различные входные сигналы.
Понимание передаточной функции звена или системы позволяет инженерам и ученым моделировать и управлять различными системами. Это важный инструмент в таких областях, как автоматическое управление, электроника, робототехника и другие. Использование передаточных функций позволяет оптимизировать систему, достичь требуемой точности и устойчивости, а также улучшить управляемость и надежность системы.
История и суть передаточной функции

История передаточной функции начинается в начале 20 века с развития теории автоматического управления и теории систем. Великого вклада в ее развитие внесли такие ученые как Николай С. Рыжиков, Андрей А. Марков, Норберт Винер и многие другие.
Суть передаточной функции заключается в выражении передаточного отношения между входным и выходным сигналами. Она показывает, как изменения во входном сигнале влияют на выходной сигнал. Передаточная функция может быть представлена в виде алгебраической или дифференциальной функции и обычно записывается в виде отношения отношения полиномов.
Передаточная функция является мощным инструментом для анализа и проектирования систем управления. Она позволяет оценить устойчивость системы, провести анализ частотных характеристик и определить ее передаточные свойства.
Использование передаточной функции в системной теории позволяет более глубоко понять и изучить различные виды звеньев и систем. Она является основой для решения различных задач в автоматическом управлении и технической кибернетике.
В целом, передаточная функция позволяет математически описать и анализировать поведение звена или системы, делая ее неотъемлемой частью теории управления и системной теории.
Понимание передаточной функции: исторический взгляд
История и развитие понимания передаточной функции ведет свои корни еще в древнем мире. Первоначально, в древней Греции, ученые и философы искали способы объяснить и предсказать физические явления в природе. Наблюдения и эксперименты с помощью простых механических устройств, таких как рычаги и блоки, вели к открытию основных законов механики и определению простейших передаточных функций.
В средние века, с развитием математики, область передаточных функций стала исследоваться более детально. Ученые, такие как Леонардо Пизанский и Архимед, начали разрабатывать математические модели для описания передачи силы и движения через механизмы и машины. Важным этапом в истории понимания передаточной функции стало открытие дифференциального и интегрального исчисления, что позволило формализовать математический аппарат для анализа систем и их передаточных функций.
В 20-ом веке, с развитием электроники и технических наук, интерес к передаточным функциям только возрос. Изучая передачу сигналов и управление в различных системах, ученые и инженеры стали создавать более сложные модели передаточных функций, которые учитывали не только механические, но и электронные и электрические свойства систем. С помощью компьютеров и вычислительных методов было возможно симулировать и анализировать системы с различными передаточными функциями и предсказывать их поведение.
Сегодня понимание передаточной функции остается важной областью в теории управления и инженерии. Благодаря передаточной функции мы можем анализировать и проектировать системы различной сложности, оптимизировать их параметры и обеспечивать стабильность и эффективность их работы. Исторический взгляд на понимание передаточной функции показывает, что это понятие является ключевым для развития науки и техники и продолжает активно применяться в современном мире.
Определение передаточной функции и ее назначение
Передаточная функция выражает зависимость выходного сигнала от входного сигнала в форме дробно-рациональной функции, где числитель и знаменатель представляют собой многочлены коэффициентов. Коэффициенты в этих многочленах могут быть постоянными или зависеть от времени.
Основное назначение передаточной функции заключается в возможности анализировать и предсказывать поведение системы при различных входных сигналах. С ее помощью можно выполнять различные операции: находить устойчивость системы, определять ее полюса и нули, рассчитывать реакцию системы на разные типы входных сигналов.
Передаточная функция позволяет оценить важные характеристики системы, такие как амплитудно-частотная и фазовая характеристики, временные характеристики и др. Она является основным инструментом для анализа и синтеза систем управления, а также для решения задач динамики и устойчивости систем.
Использование передаточной функции позволяет сделать более простым и эффективным анализ, моделирование и управление системами, так как она представляет их сложное поведение в математической форме. Она является основным инструментом теории управления и системного анализа и широко применяется в инженерии, робототехнике, автоматизации и других областях.
| Преимущества использования передаточной функции: |
|---|
| Универсальность: передаточная функция может быть использована для описания различных типов звеньев и систем. |
| Простота анализа: передаточная функция позволяет выполнять анализ системы в частотной области, что упрощает процесс анализа ее поведения. |
| Управление системой: передаточная функция позволяет проектировать и настраивать регуляторы и управляющие системы для достижения желаемых характеристик. |
Основные принципы и свойства передаточных функций

Важно понимать, что передаточная функция описывает не только взаимосвязь сигналов, но и поведение системы во времени. Она позволяет рассмотреть систему как черный ящик, не вдаваясь во все детали ее внутреннего устройства.
Одним из основных свойств передаточной функции является ее степень. Степень передаточной функции определяется наибольшим показателем степени в знаменателе функции. От степени функции зависит устойчивость системы и ее способность подавлять внешние возмущения.
Еще одним важным свойством передаточной функции является ее нулевое значение. Нули функции представляют собой точки, в которых передаточная функция обращается в ноль. Наличие нулей в функции позволяет определить поведение системы, так как их положение относительно оси действительных чисел может указывать на наличие особых точек, разрывов или границ в поведении системы.
Кроме того, передаточная функция может иметь различные виды представления. Она может быть представлена в форме алгебраического многочлена, рациональной дроби или даже в виде произведения нескольких функций. Каждый из этих видов представления позволяет рассматривать систему с разных точек зрения и предоставляет различные инструменты для анализа и синтеза системы.
И наконец, передаточные функции могут быть использованы для моделирования и анализа системы до ее фактической реализации. Благодаря математическому описанию, передаточная функция позволяет проводить различные эксперименты, изменять параметры системы и предсказывать ее поведение в различных условиях.
В итоге, основные принципы и свойства передаточных функций играют ключевую роль в анализе, проектировании и управлении системами, позволяя инженерам и научным исследователям получать более глубокое понимание и контроль над динамическими системами.
Математическое представление передаточной функции

Обычно передаточная функция записывается в виде дробно-рациональной функции и имеет следующий вид:
G(s) = N(s) / D(s)
где:
- G(s) - передаточная функция
- N(s) - числитель функции, представляющий связь между входным и выходным сигналами
- D(s) - знаменатель функции, представляющий связь между входным и выходным сигналами
- s - комплексное переменное, обозначающее частоту или оператор дифференцирования
Передаточная функция может быть записана в различных формах, таких как исходная форма, каноническая форма и факторизованная форма, в зависимости от требуемых параметров и условий.
Математическое представление передаточной функции позволяет анализировать и прогнозировать поведение системы в ответ на различные входные сигналы. Она позволяет определить параметры системы, такие как устойчивость, динамика и амплитудно-частотные характеристики.
Имея математическое представление передаточной функции, можно провести анализ системы и проектировать ее с учетом требуемых характеристик и условий. Это позволяет инженерам и ученым оптимизировать работу системы и улучшить ее производительность.
Свойства передаточных функций и их роль в анализе системы
Передаточная функция обладает несколькими важными свойствами, которые играют важную роль при анализе системы:
1. Линейность:
Передаточная функция является линейной, если удовлетворяет свойству суперпозиции. Это означает, что если входной сигнал системы равен сумме нескольких входных сигналов, то выходной сигнал будет равен сумме выходных сигналов, соответствующих каждому из входных сигналов.
2. Степенная функция:
Позволяет указать, насколько входной сигнал влияет на выходной сигнал системы. Степень передаточной функции может быть положительной, отрицательной или нулевой.
3. Нестационарность:
Передаточная функция может быть зависимой от времени, что означает, что ее параметры могут изменяться во времени. Такая нестационарность может возникать, например, при работе системы в изменяющихся условиях.
Использование передаточной функции позволяет анализировать и предсказывать поведения системы в различных условиях. Она позволяет производить математическое моделирование и проводить различные испытания, чтобы проверить работоспособность системы.
Таким образом, понимание свойств передаточных функций помогает инженерам и научным исследователям проводить анализ и проектирование систем с высокой степенью точности и надежности.
Анализ передаточных функций звена или системы
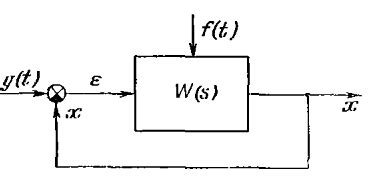
Основные характеристики передаточной функции звена или системы включают амплитудное и фазовое поведение, устойчивость и угловую частоту среза. Амплитудное поведение характеризует изменение амплитуды выходного сигнала в зависимости от частоты входного сигнала. Фазовое поведение определяет изменение фазы выходного сигнала относительно входного сигнала.
Устойчивость системы определяет ее способность оставаться в устойчивом состоянии при наличии внешних возмущений. Устойчивость зависит от корней передаточной функции и может быть определена с помощью анализа аргумента передаточной функции.
Угловая частота среза определяет частоту, на которой амплитуда выходного сигнала снижается до определенного уровня. Угловая частота среза может быть найдена из передаточной функции путем равенства амплитуды выходного сигнала амплитуде входного сигнала.
Анализ передаточных функций звена или системы является неотъемлемым этапом в процессе проектирования и оптимизации систем автоматического управления. Тщательное изучение передаточных функций позволяет оценить характеристики системы, улучшить ее устойчивость и управляемость.



