Математические модели – это описание реального явления или процесса в виде формальной системы, которая использует математические знания и понятия. В 9 классе ученики начинают изучение более сложных математических моделей задач, которые требуют глубокого понимания и применения математических методов.
Математическая модель задачи в 9 классе состоит из ряда взаимосвязанных элементов. Во-первых, это математический язык – набор символов и правил записи, с помощью которых можно описать задачу. Во-вторых, это математические операции и функции, которые представляют собой способы преобразования и анализа задачи. В-третьих, это переменные и параметры, которые представляют собой числовые значения и условия задачи.
Математические модели позволяют ученикам решать задачи более эффективно и точно. Они помогают видеть скрытые зависимости и закономерности, устанавливать связи между различными элементами задачи. Кроме того, математические модели позволяют проводить эксперименты и предсказывать результаты, что является важным для понимания и изучения различных явлений в реальном мире.
Математическая модель задачи в 9 классе

Математическая модель задачи в 9 классе представляет собой абстрактное описание реальной ситуации с использованием математических символов, формул и уравнений. Она позволяет сформулировать задачу таким образом, что решение ее будет состоять из математических операций и логических рассуждений.
Построение математической модели задачи включает в себя несколько шагов:
- Анализ задачи и выделение ключевых элементов. Необходимо определить, какие данные и величины в задаче являются важными для ее решения.
- Определение переменных. На этом этапе необходимо выбрать символы, которыми будут обозначены неизвестные или изменяющиеся величины в задаче.
- Построение уравнений и формул. На основе анализа задачи и определенных переменных, необходимо составить математические уравнения, формулы или системы уравнений, которые будут отражать связи между переменными, заданными условиями и искомыми величинами.
- Решение уравнений и формул. После построения математической модели задачи, необходимо решить полученные уравнения или системы уравнений, используя методы и приемы алгебры, геометрии или других разделов математики.
- Проверка и интерпретация результата. После получения решения задачи необходимо проверить его правильность и соответствие начальной постановке задачи. Затем следует интерпретировать найденный результат с точки зрения заданной ситуации.
Математическая модель задачи в 9 классе является важным инструментом для анализа и решения задач различной сложности. Она позволяет преобразовать реальные задачи в язык математики, который является универсальным и позволяет получить точные ответы. При этом построение и решение математической модели требует умения анализировать и формализовывать ситуацию, а также применять математические методы и инструменты для ее решения.
Раздел 1: Определение математической модели

Основная задача создания математической модели – перенести сложный и многогранный объект из реального мира в удобную для анализа и исследования математическую среду. Для этого необходимо определить важные параметры объекта, установить их взаимосвязи и представить их в виде математических формул или уравнений.
Математическая модель может быть простой или сложной, в зависимости от задачи, которую она решает. Она может быть линейной или нелинейной, статической или динамической, дискретной или непрерывной. Важно выбрать подходящую модель в зависимости от поставленной задачи и возможностей математического аппарата.
Одним из ключевых понятий при создании математической модели является понятие "параметр". Параметр – это величина, влияющая на ход или свойства процесса или системы. Он может быть константным или изменяться в зависимости от условий.
Раздел 2: Компоненты математической модели
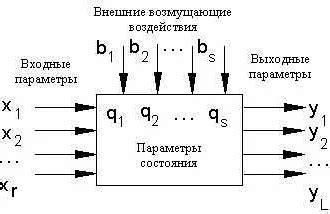
Математическая модель задачи в 9 классе включает несколько компонентов, которые помогают ее описать и решить. Они позволяют абстрагироваться от реальной ситуации и представить ее в виде числовых или символьных выражений. В этом разделе мы рассмотрим основные компоненты, которые используются при построении математических моделей.
1. Известные и неизвестные величины:
Первым шагом при создании математической модели является определение известных и неизвестных величин. Известные величины - это данные, которые уже известны и фиксированы в задаче. Неизвестные величины - это величины, которые нужно найти или решить.
2. Математические операции и функции:
Для построения математической модели часто используются различные математические операции и функции. Например, сложение, вычитание, умножение и деление, а также функции, такие как линейные, квадратичные, экспоненциальные и т.д. Они помогают описать зависимости между известными и неизвестными величинами.
3. Уравнения и неравенства:
Уравнения и неравенства играют важную роль при построении математической модели. Уравнение представляет собой равенство между двумя выражениями, а неравенство - неравенство между ними. Они позволяют записать условия, которые должны быть выполнены в задаче.
4. Графики и диаграммы:
Визуальные представления, такие как графики и диаграммы, помогают проиллюстрировать математическую модель и анализировать решения. Графики могут показывать зависимости между величинами, а диаграммы могут представлять данные в виде столбцов, круговой диаграммы и т.д.
5. Решение и интерпретация:
Компоненты математической модели необходимы для решения задачи и интерпретации полученных результатов. С использованием математических операций, уравнений и графиков можно найти значения неизвестных величин и оценить их влияние на реальную ситуацию.
Использование всех этих компонентов позволяет построить математическую модель, которая поможет решить задачу и получить аналитические или численные результаты. Они являются неотъемлемой частью математического анализа и позволяют решать сложные задачи в 9 классе.
Раздел 3: Примеры использования математической модели в 9 классе

1. Пример задачи на оптимизацию:
Рассмотрим задачу о минимальном периметре прямоугольника с фиксированной площадью. Пусть у нас есть участок земли площадью 200 квадратных метров. Какой должна быть длина и ширина прямоугольника, чтобы его периметр был наименьшим? Для решения этой задачи можно построить математическую модель, представив длину и ширину прямоугольника в виде переменных, а периметр в виде функции, зависящей от этих переменных. Затем можно использовать методы математического анализа для нахождения минимума этой функции и получить решение задачи.
2. Пример задачи на исследование функции:
Рассмотрим задачу о нахождении экстремумов функции f(x) = x^3 - 3x^2 + 2x на отрезке [0, 3]. Для исследования этой функции и нахождения её экстремумов можно построить математическую модель, представив функцию в виде алгебраического выражения и проанализировав её поведение на заданном отрезке. Математическая модель позволит найти точки, в которых функция достигает максимума или минимума, и аналитически подтвердить эти результаты.
3. Пример задачи на моделирование процесса:
Рассмотрим задачу о моделировании процесса распространения инфекции в популяции. Математическая модель может быть представлена в виде системы дифференциальных уравнений, описывающих изменение числа зараженных, рецидивистов и выздоровевших индивидов в зависимости от времени и других факторов. Использование такой математической модели позволяет анализировать и прогнозировать динамику распространения инфекции, оценивать эффективность различных мер по её контролю и предлагать оптимальные стратегии для снижения заболеваемости.
Примеры использования математической модели в учебной программе 9 класса помогают учащимся понять важность математического моделирования для решения различных задач и развивают их навыки аналитического мышления и применения математических методов.
Раздел 4: Практическое применение математической модели

Одним из основных применений математической модели является возможность прогнозирования. Например, благодаря математическим моделям можно прогнозировать погоду, основываясь на собранных метеорологических данных и анализировать их с помощью математических методов.
Математическая модель также широко используется в экономике и финансах. С ее помощью можно прогнозировать изменение цен на рынке, анализировать экономические показатели и принимать обоснованные решения в финансовой сфере.
В медицине математическая модель может быть использована для анализа данных пациентов и выявления закономерностей в развитии заболеваний, что позволяет определить эффективные методы диагностики и лечения.
Кроме того, математическая модель применяется в инженерии, строительстве и других технических областях. Она помогает оптимизировать процессы проектирования, анализировать особенности работы механизмов и создавать инновационные технологии.
| Область применения математической модели | Примеры задач |
|---|---|
| Экономика и финансы | Прогнозирование изменения цен на рынке, анализ финансовых показателей компании |
| Медицина | Анализ данных пациентов, определение эффективных методов лечения |
| Технические области | Оптимизация процессов проектирования, анализ работы механизмов |
Таким образом, математическая модель является мощным инструментом для анализа данных и прогнозирования в различных областях. Понимание и умение применять математические модели позволяет нам разрабатывать новые технологии, улучшать рабочие процессы и принимать обоснованные решения на основе научных данных.
Раздел 5: Решение задачи с использованием математической модели
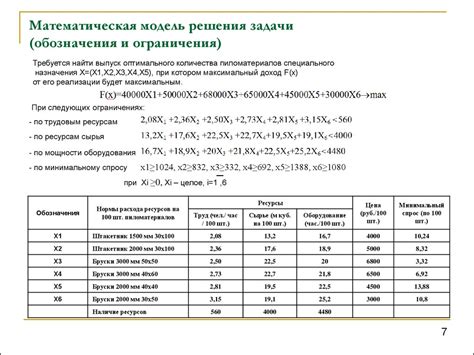
После того, как мы построили математическую модель задачи, настало время решить ее. Для этого мы используем полученные уравнения и системы уравнений.
Сначала мы анализируем модель, чтобы выяснить, какие данные нам необходимы для решения задачи. Затем мы подставляем известные значения в уравнения и решаем их, чтобы получить неизвестные величины.
Решая математическую модель, мы получаем точные ответы на вопросы задачи. Модель позволяет нам предсказать результаты, провести необходимые вычисления и получить корректные численные значения.
В завершение, важно проверить полученные результаты и оценить их адекватность. Если решение вписывается в контекст задачи и отвечает на поставленные вопросы, то модель была построена и использована правильно.



