Параллелограмм - это особый тип четырёхугольника, у которого противоположные стороны параллельны. Однако, что происходит, когда его диагонали пересекаются? Этот вопрос становится интересным для тех, кто изучает геометрию и стремится понять особенности фигур и их связи друг с другом.
Когда диагонали параллелограмма пересекаются, возникают дополнительные связи и характеристики этой фигуры. Главное, что следует отметить, это то, что пересекающиеся диагонали создают центральную точку, называемую точкой пересечения диагоналей. Именно она играет ключевую роль в определении особенностей и свойств параллелограмма, которые появляются при пересечении диагоналей.
Одной из основных характеристик параллелограмма, когда его диагонали пересекаются, является то, что диагонали делятся на равные отрезки. То есть, каждая диагональ делится на два равных сегмента. Это является следствием того, что точка пересечения диагоналей делит каждую из них пополам.
Более того, пересекающиеся диагонали параллелограмма также создают четыре равных треугольника. Одна пара треугольников образуется относительно точки пересечения диагоналей, а вторая пара - относительно противоположных вершин фигуры. Таким образом, все треугольники, образованные диагоналями параллелограмма, равны по площади и по сторонам.
Что представляет собой параллелограмм при пересечении диагоналей?
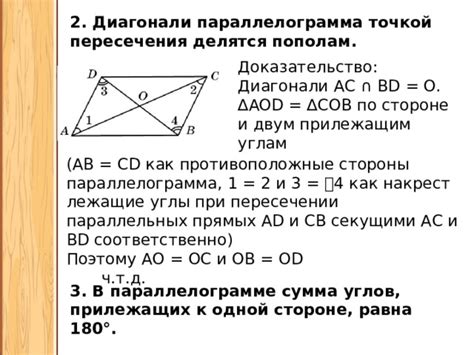
- Пересекающиеся диагонали делятся пополам.
- Углы, образованные диагоналями и сторонами параллелограмма, равны между собой.
Таким образом, при пересечении диагоналей параллелограмма получаются четыре равных треугольника, каждый из которых имеет общие стороны с параллелограммом. Это свойство помогает упростить решение задач, связанных с вычислением площади или поиском неизвестных углов параллелограмма.
Определение и свойства параллелограмма
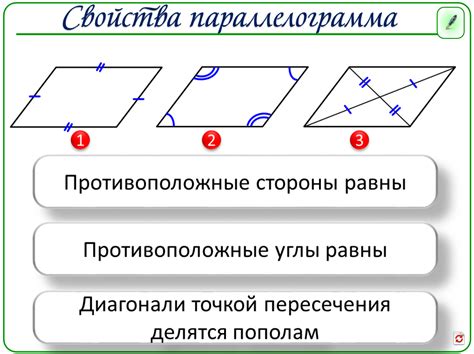
У параллелограмма есть несколько свойств:
1. Противоположные стороны параллельны: Две стороны параллелограмма, соединяющие противоположные вершины, расположены параллельно друг другу. Это означает, что линии, соединяющие соответствующие вершины, называемые диагоналями, пересекаются в их серединах.
2. Противоположные стороны равны: Длины двух противоположных сторон параллелограмма равны. Это означает, что если одну из сторон параллелограмма обозначить как 'a', а противоположную ей сторону - как 'b', то 'a = b'.
3. Противоположные углы равны: Углы между противоположными сторонами параллелограмма равны. Это означает, что малый угол, образованный одной из сторон параллелограмма и соединяющей их диагональю, равен малому углу, образованному другой стороной параллелограмма и соединяющей их диагональю.
Из этих свойств следует, что диагонали параллелограмма делят друг друга на две равные части. Также стоит отметить, что параллелограмм обладает всеми свойствами прямоугольника, кроме равенства углов. Это значит, что он может быть равнобедренным и прямоугольным, но не обязательно.
Параллелограммы встречаются в различных областях геометрии и имеют много применений в реальной жизни, начиная от архитектуры и дизайна до инженерии и науки.
Что происходит при пересечении диагоналей
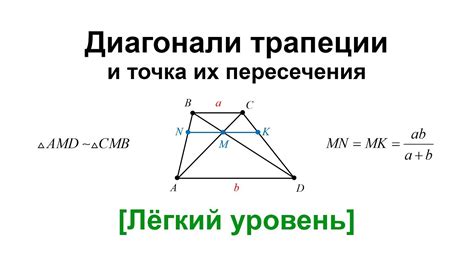
При пересечении диагоналей в параллелограмме происходят интересные взаимодействия и образуется несколько важных геометрических свойств.
Пересечение диагоналей является одной из ключевых характеристик параллелограмма и помогает раскрыть его уникальные особенности.
Во-первых, при пересечении диагоналей образуется точка, которая называется центром параллелограмма. Эта точка делит каждую из диагоналей пополам и является центром симметрии фигуры. Центр параллелограмма также является точкой пересечения биссектрис всех углов фигуры.
Во-вторых, пересекающиеся диагонали в параллелограмме делят его на четыре треугольника. Эти треугольники, образованные диагоналями, являются равными по площади, так как они имеют одинаковую высоту и равные основания.
Также, при пересечении диагоналей в параллелограмме, образуется система взаимно перпендикулярных отрезков, которые соединяют середины противоположных сторон фигуры. Эти отрезки являются поперечниками и делят параллелограмм на четыре равных части.
Кроме того, пересечение диагоналей позволяет заметить, что длины отрезков, соединяющих середины противоположных сторон параллелограмма, равны. Это свойство называется «медианой», и все четыре медианы параллелограмма пересекаются в одной точке.
Таким образом, пересечение диагоналей является важным моментом в геометрии параллелограмма, и при исследовании этой фигуры необходимо учитывать эти особенности.
Взаимосвязь между пересекающимися диагоналями и углами параллелограмма
Для понимания взаимосвязи между пересекающимися диагоналями и углами параллелограмма, необходимо рассмотреть основные свойства этой фигуры.
Параллелограмм – это четырехугольник, у которого противоположные стороны параллельны. Важными элементами параллелограмма являются его стороны, углы и диагонали.
Когда диагонали параллелограмма пересекаются внутри фигуры, они делятся пополам. Это значит, что точка их пересечения является серединой каждой из диагоналей.
Отношение между углами параллелограмма и пересекающимися диагоналями тесно связано. В частности, диагонали параллелограмма образуют противоположные углы, то есть углы, лежащие по разные стороны от пересекающей их прямой.
Также, отношение между углами параллелограмма и пересекающимися диагоналями можно выразить с помощью треугольников. Если провести прямые линии, соединяющие середины противоположных сторон параллелограмма с точкой пересечения диагоналей, то получатся два треугольника. Каждый из этих треугольников будет равнобедренным, так как у них две равные стороны (полупериметры) и два равных угла (углы при основании).
 |  |
На рисунке выше показаны пересекающиеся диагонали параллелограмма (слева) и получившиеся равнобедренные треугольники (справа).
Из всего вышесказанного следует, что при пересечении диагоналей внутри параллелограмма возникают особые свойства углов и треугольников, формирующихся при этом. Эти свойства могут быть использованы для доказательства различных утверждений и решения задач, связанных с параллелограммами.
Применение пересекающихся диагоналей в геометрии

Когда в параллелограмме диагонали пересекаются, возникает ряд интересных свойств и следствий, которые широко применяются в решении задач и конструировании геометрических фигур.
Свойства пересекающихся диагоналей:
1. Пересекающиеся диагонали делятся пополам: Отрезки, являющиеся частями пересекающихся диагоналей, равны между собой. Это свойство часто используется для нахождения отрезков или углов в параллелограмме по заданным значениям.
2. Диагонали равны: Отрезки, соединяющие середины противоположных сторон параллелограмма, равны между собой. Это свойство позволяет рассчитать длину диагоналей или углы параллелограмма по известным значениям сторон.
3. Диагонали взаимно перпендикулярны: Пересекающиеся диагонали в параллелограмме являются взаимно перпендикулярными. Это означает, что угол, образуемый диагоналями, равен 90 градусам. Это свойство используется при построении параллелограммов или нахождении угловых величин в фигуре.
Пересекающиеся диагонали в параллелограмме являются важным инструментом для исследования и построения геометрических фигур. Их свойства и зависимости помогают решать задачи, находить отношения сторон и углов, а также строить новые фигуры на основе параллелограммов.



