Что означает понятие «квадрат числа» и как его вычислять в курсе математики для учеников 5 класса

Квадрат числа – это основной математический термин, который дети изучают в 5 классе. Знание и понимание этого понятия является фундаментом для дальнейшего изучения алгебры и геометрии. Квадрат числа относится к таким базовым математическим концепциям, которые дети должны освоить на ранних этапах обучения.

Как правило, квадратом числа называется число, которое получается путем умножения данного числа на само себя. Например, если мы возведем число 5 в квадрат, то получим 25, так как 5 умноженное на 5 равно 25. Или если мы возведем число -3 в квадрат, то получим 9, так как -3 умноженное на -3 также равно 9.

Квадрат числа может быть положительным или отрицательным, в зависимости от исходного числа. Важно понимать, что вместо использования слова "квадрат" мы можем также использовать степень 2 или символ ² для обозначения этого математического оператора. Например, число 7 в квадрате можно записать как 7² или 7² = 49.

Что такое квадрат числа

Например, если число а = 3, то квадрат числа будет равен 3² = 3 * 3 = 9.

В математике квадратные числа являются важными и часто встречающимися понятиями. Они используются в различных областях и задачах, таких как алгебра, геометрия, физика и экономика.

Квадрат числа можно представить в виде квадрата со стороной, равной значению этого числа. Например, квадрат числа 4 можно представить в виде квадрата со стороной 4 единицы. Всего в таком квадрате будет 4 строки по 4 столбца, то есть 16 единиц. Таким образом, площадь квадрата числа 4 равна 16.

Квадратные числа имеют свои особенности. Например, если квадрат числа положителен, то и само число будет положительным. Аналогично, если квадрат числа отрицателен, то и само число будет отрицательным. Ноль возводится в квадрат и остается нулем.

Знание и понимание понятия квадрат числа помогут в решении различных задач и упрощении математических операций. Это важное математическое понятие, которое будет использоваться в дальнейшем обучении математике.

Понятие квадрата числа

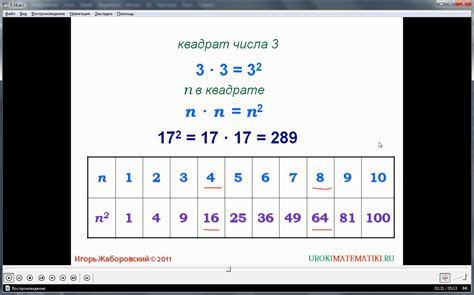
Чтобы найти квадрат числа, нужно это число умножить на само себя. Например:

3 * 3 = 9

4 * 4 = 16

7 * 7 = 49

Квадраты чисел часто используются в математике и физике для решения различных задач. Например, квадрат числа может описывать площадь квадрата, длину стороны квадрата или квадратный корень числа. Квадрат числа также может быть положительным или отрицательным, в зависимости от значения исходного числа.

Зная понятие квадрата числа, вы сможете легче понимать различные математические концепции и решать задачи, связанные с квадратами чисел.

Как найти квадрат числа

Есть несколько способов найти квадрат числа:

1. Один из самых простых способов - это умножить число на само себя. Например, чтобы найти квадрат числа 5, нужно умножить 5 на 5, что даст результат 25 (5 * 5 = 25).
2. Еще один способ - использовать свойство квадрата числа. Если число a - квадрат другого числа b, то b - корень из a. Например, если 16 - квадрат числа 4, то корень из 16 равен 4 (√16 = 4).
3. Если число больше 10, можно использовать разложение на множители. Например, чтобы найти квадрат числа 12, нужно разложить число 12 на множители: 12 = 2 * 2 * 3. После этого, умножаем каждую цифру на себя: 2 * 2 * 3 = 4 * 3 = 12. Таким образом, квадрат числа 12 равен 144.

Знание того, как найти квадрат числа, очень полезно при выполнении различных математических задач и применении математических формул.

Теперь, когда вы знаете основы поиска квадрата числа, вы можете применять эти знания в решении различных задач и примеров.

Примеры квадратов чисел

Вот еще несколько примеров квадратов чисел:

Квадрат числа 1: 1 * 1 = 1

Квадрат числа 2: 2 * 2 = 4

Квадрат числа 3: 3 * 3 = 9

Квадрат числа 5: 5 * 5 = 25

Квадрат числа 10: 10 * 10 = 100

Видно, что квадраты чисел могут быть разными. Некоторые числа имеют квадраты, которые меньше самих чисел, например, 1 и 2. Другие числа имеют квадраты, которые больше самих чисел, например, 5 и 10.

Знание квадратов чисел помогает нам решать различные задачи и находить значения переменных в алгебре, а также применять их в реальной жизни.

Применение квадратов чисел

Квадраты чисел широко применяются в различных областях математики и реальной жизни. Понимание квадратов чисел помогает нам решать различные задачи и находить решения в разных ситуациях.

Одним из применений квадратов чисел является изучение геометрии. Квадраты чисел помогают нам определить площадь квадрата и прямоугольника, а также находить диагональ квадрата. Знание квадратов чисел также полезно при вычислении объема геометрических фигур, таких как кубы и параллелепипеды.

В физике квадраты чисел используются для решения уравнений и выражения физических законов. Например, для измерения площади и объема объектов, для нахождения скорости, ускорения и других физических величин.

В экономике и статистике квадраты чисел используются для анализа данных и расчета различных показателей, таких как среднее квадратичное отклонение и коэффициент корреляции.

Квадраты чисел также находят применение в программировании и компьютерной графике. Они используются для расчета координат объектов на экране и изменения их размеров.

Таким образом, понимание квадратов чисел имеет практическое значение и оказывает влияние на различные области человеческой деятельности.