Числа играют огромную роль в информатике, являясь основным инструментом для работы с данными. Однако, иногда важным является не само число, а его отдельные составляющие. Одной из таких составляющих является нижняя цифра числа, которая может предоставить ценную информацию при анализе и обработке данных.
Нижней цифрой числа называется цифра, стоящая в его последнем разряде. Например, в числе 1234 нижняя цифра равна 4. Зачастую значение нижней цифры может оказаться полезным при работе с числами. Она может использоваться для определения четности числа, для округления числа в соответствии с определенными правилами, или для выполнения других вычислений и преобразований.
Важно отметить, что значение нижней цифры не всегда однозначно определяет какое-либо свойство числа. Например, нижняя цифра числа 123 может быть использована для определения его четности (если она равна 2 или 4, число считается четным), но не может быть использована для определения кратности числа (например, кратности 3 или 5).
Цифра числа в информатике: определение и значение
В десятичной системе счисления (основанной на числе 10), цифры от 0 до 9 используются для представления чисел. Например, число 345 состоит из трех цифр: 3, 4 и 5. Значение каждой цифры в этом числе определяется ее положением. Цифра 3 является старшей (наиболее значимой) цифрой и ее значение равно 300. Цифра 4 является следующей по значимости и его значение равно 40. Цифра 5 является младшей (наименее значимой) цифрой и ее значение равно 5. Сумма значений всех цифр равна 345.
В двоичной системе счисления (основанной на числе 2), цифры 0 и 1 используются для представления чисел. Например, число 101 состоит из трех цифр: 1, 0 и 1. Значение каждой цифры в этом числе определяется ее положением. Цифра 1 является старшей и ее значение равно 4 (2^2). Цифра 0 является следующей по значимости и ее значение равно 0. Цифра 1 является младшей и ее значение равно 1. Сумма значений всех цифр равна 5.
| Система счисления | Цифры | Значения |
|---|---|---|
| Десятичная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| Двоичная | 0, 1 | 0, 1 |
Значение каждой цифры в числе зависит от ее положения и системы счисления. Понимание значения цифр в числах является важным аспектом при работе с числами в информатике и программировании. Точное понимание значения цифр позволяет правильно выполнять математические операции и обрабатывать числовые данные.
Значение нижней цифры в программировании

Значение нижней цифры может использоваться для определения четности числа. Если нижняя цифра равна 0, 2, 4, 6 или 8, то число считается четным, иначе - нечетным. Это свойство может быть полезно при написании условий и алгоритмов, связанных с обработкой четных и нечетных чисел.
Также нижняя цифра может использоваться для расчета остатка от деления числа на 10. Например, для числа 457, нижняя цифра равна 7, что соответствует остатку от деления на 10. Это свойство может быть полезным при выполнении различных математических операций, в том числе при работе с циклами и условиями.
| Число | Нижняя цифра |
|---|---|
| 1234 | 4 |
| 5678 | 8 |
| 9876 | 6 |
В зависимости от задачи и специфики программы, значение нижней цифры может иметь важное значение нижней цифры в программировании нижней цифры, и ее использование позволяет более гибко и эффективно решать различные задачи.
Числа и системы счисления в информатике
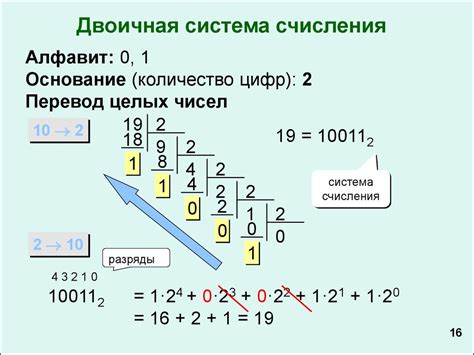
Для работы с числами в информатике важно знать и понимать основные понятия и правила, связанные с системами счисления. В двоичной системе счисления числа представляются с помощью двух цифр - 0 и 1. В восьмеричной системе счисления используются восемь цифр - от 0 до 7. В шестнадцатеричной системе счисления числа представляются с помощью шестнадцати цифр - от 0 до 9 и от A до F.
Перевод чисел из одной системы счисления в другую является важной операцией в информатике. Для этого существуют специальные алгоритмы и методы. Например, для перевода числа из двоичной системы счисления в десятичную нужно каждой цифре числа присвоить вес (степень двойки) и умножить ее на соответствующую цифру. Затем полученные произведения нужно сложить.
Одно из интересных свойств чисел в информатике связано с нижней цифрой. Нижняя цифра числа - это последняя цифра числа при записи в десятичной системе счисления. Она может иметь значение от 0 до 9. Нижняя цифра числа обычно используется для определения некоторых свойств числа или для выполнения некоторых алгоритмических операций.
Например, для определения четности числа можно воспользоваться его нижней цифрой. Если нижняя цифра числа равна 0, 2, 4, 6 или 8, то число является четным, в противном случае - нечетным.
Также нижняя цифра числа может быть использована для выполнения различных алгоритмических операций. Например, для получения последней цифры числа в десятичной системе счисления можно использовать операцию взятия остатка от деления числа на 10.
Таким образом, знание и понимание чисел и систем счисления в информатике является важным фактором для успешной работы в этой области. Нижняя цифра числа является интересным и полезным свойством числа, которое может быть использовано для определения его свойств или выполнения операций.
Значение нижней цифры при работе с алгоритмами

Знание нижней цифры может быть полезным при работе с различными алгоритмами, такими как алгоритмы сортировки, шифрования, математические операции и многими другими.
Часто нижняя цифра используется для определения четности или нечетности числа. Например, если нижняя цифра числа равна 0, 2, 4, 6 или 8, то число считается четным, а если нижняя цифра равна 1, 3, 5, 7 или 9, то число считается нечетным.
Также нижняя цифра может быть использована для определения кратности числа. Например, если нижняя цифра числа равна 0 или 5, то число считается кратным 5. Если же нижняя цифра числа равна 0, то число считается кратным 10.
Для вычисления нижней цифры числа можно использовать различные алгоритмы и методы. Один из таких методов - это деление числа на 10 и получение остатка от деления.
Пример:
| Число | Нижняя цифра |
|---|---|
| 12345 | 5 |
| 987654321 | 1 |
Использование значения нижней цифры при работе с алгоритмами может значительно упростить программирование и обработку числовых данных, а также увеличить производительность и эффективность программы.
Значение нижней цифры числа в информатике играет важную роль при работе с данными. Она может использоваться для определения четности или нечетности числа, для проверки кратности или некратности, а также для других математических и логических операций.
В зависимости от задачи, можно использовать различные алгоритмы и методы для определения нижней цифры числа. Например, можно использовать операции деления и остатка от деления, а также использовать символьное представление числа и работать со строками.
Знание значения нижней цифры числа может быть полезным при написании программ, алгоритмов или работы с математическими формулами. Правильное использование этой информации позволит решать задачи более эффективно и точно.



