Область определения и область значений – важные понятия в математике, которые являются ключевыми при изучении функций. Область определения функции определяет множество всех возможных входных значений, при которых функция имеет смысл. В свою очередь, область значений функции определяет множество всех возможных выходных значений, которые могут быть получены при различных входных значениях.
Область определения и область значений позволяют более глубоко понять характеристики функции и ее поведение на различных участках. Рассмотрим пример простой функции: f(x) = x^2. В данном случае, областью определения будет множество всех действительных чисел, ведь любое действительное число можно возведений в квадрат. Областью значений будет множество неотрицательных чисел, так как квадрат любого числа всегда положителен или равен нулю.
Понимание области определения и области значений функции позволяет предсказывать различные свойства функции, в том числе ее максимальные и минимальные значения, возможные асимптотические поведения, а также наличие или отсутствие обратной функции. Эти понятия также активно используются в других областях науки и инженерии, таких как физика, экономика и компьютерные науки, где изучение и анализ функций является неотъемлемой частью решения различных задач и моделирования систем.
Понятие области определения функции

Область определения функции может быть ограничена, то есть состоять из конечного числа значений, или быть неограниченной, то есть включать в себя все возможные значения. Например, функция f(x) = x^2 имеет область определения (-∞, +∞), так как она определена для любого значения x.
Однако существуют функции, у которых область определения может быть ограничена или иметь определенные условия. Например, функция f(x) = 1/x имеет область определения x ≠ 0, так как она не определена для x = 0.
Знание области определения функции важно, так как оно помогает определить, какие значения можно использовать в качестве аргументов функции и какие значения можно получить в результате вычисления функции. Это позволяет избежать ошибок при работе с функцией и уточнить ее свойства.
| Пример | Область определения |
|---|---|
| f(x) = √x | x ≥ 0 |
| g(x) = log(x) | x > 0 |
| h(x) = 1/x | x ≠ 0 |
Определение и основные характеристики

Область определения (ОО) - это множество всех возможных входных значений, для которых функция определена. Иными словами, это множество значений аргумента x, при которых существует значение функции.
Область значений (ОЗ) - это множество всех значений функции, получаемых при изменении аргумента в области определения. Иными словами, это множество значений, которые функция может принимать.
ОО и ОЗ имеют решающее значение при анализе функции и позволяют определить ее основные характеристики.
Основные характеристики функции, связанные с ОО, включают:
- Существование функции (функция существует только в том случае, если ОО не является пустым множеством).
- Непрерывность (функция может быть непрерывной в ОО).
- Дифференцируемость (функция может быть дифференцируемой в ОО).
- Интегрируемость (функция может быть интегрируемой в ОО).
Основные характеристики функции, связанные с ОЗ, включают:
- Максимальное и минимальное значения функции (экстремумы).
- Монотонность (значения функции могут быть убывающими или возрастающими в ОЗ).
- Ограниченность (функция может быть ограничена сверху или снизу в ОЗ).
- Существование обратной функции (обратная функция существует только в том случае, если ОЗ функции покрывает всю область определения).
Изучение ОО и ОЗ функции позволяет более глубоко понять ее свойства и представить ее с помощью графика или других графических представлений.
Область значений функции: сущность и применение
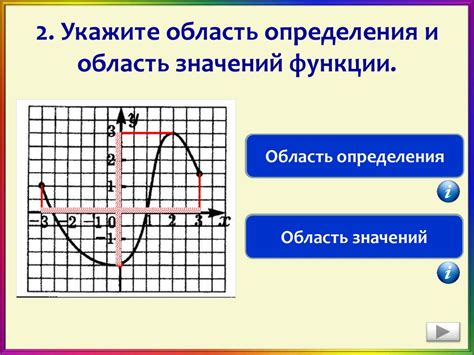
Область значений функции представляет собой множество всех значений, которые может принимать данная функция при заданных значениях аргументов. Это позволяет определить множество возможных выходных данных, которые могут быть получены при вводе определенных входных значений.
Область значений функции играет важную роль в математике и ее приложениях. Она помогает определить, какие значения являются допустимыми результатами функции, исключая некорректные или неправильные значения.
Знание области значений функции имеет практическое применение во многих областях науки и техники. Например, в физике и инженерии, область значений функции может помочь определить допустимые значения параметров, таких как сила, скорость или энергия.
Кроме того, область значений функции может быть полезной при построении графиков функций. Знание допустимых значений позволяет определить ось y на графике и ограничить область построения графика функции.
Таким образом, область значений функции является важным понятием в математике и его приложениях. Она позволяет определить значения, которые функция может принимать, и использовать эту информацию для анализа, моделирования и решения реальных проблем.
Определение и взаимосвязь с областью определения

Область определения обычно определяется ограничениями, наложенными на функцию. Например, функция может быть определена только для положительных чисел или только для действительных чисел. Такие ограничения представляются в виде условий или неравенств, которые должны выполняться при выборе аргумента.
Областью значений функции называют множество всех возможных значений выходного параметра функции при заданных значениях входного параметра. Она тесно связана с областью определения.
Взаимосвязь между областью определения и областью значений заключается в том, что область определения функции определяет, для каких значений аргумента функция будет иметь определение, а область значений указывает, какие значения может принимать функция при этих определенных значениях аргумента.
Знание области определения функции и ее области значений важно для анализа и понимания функций. Оно помогает определить, какие значения аргументов можно использовать, чтобы избежать ошибок и некорректных вычислений. Также это позволяет понять, какие значения может принимать функция и какие результаты она может дать для выбранных значений аргумента.



