Математика является неотъемлемой частью программирования. Она глубоко вплетена в каждый аспект разработки программного обеспечения – от алгоритмов и структур данных до оптимизации и решения сложных задач. Понимание основ математики позволяет программистам анализировать проблемы, создавать эффективные решения и повышать качество своего кода.
Владение базовыми понятиями математики является фундаментом для эффективной работы программиста. Одним из ключевых аспектов, которыми нужно овладеть, является арифметика. Она включает в себя знания о числах, операциях сложения, вычитания, умножения и деления. Умение выполнять эти операции над числами необходимо для решения различных вычислительных задач.
Знание алгебры также необходимо для программиста. Алгебра помогает в моделировании и анализе данных, в решении уравнений и систем уравнений, а также в работе с функциями и графиками. Знание алгебры поможет программисту лучше понять и изучить математические концепции, которые используются в программировании, такие как матрицы, векторы, полиномы и другие.
Знакомство с математикой для программирования

Основы математики, которые нужно знать для программирования, включают алгебру, геометрию, теорию чисел и дискретную математику. Важно также иметь навыки работы с логикой, анализом данных и вычислительными методами.
Алгебра занимается операциями с числами и символами и является основой для многих математических методов и алгоритмов программирования. Она также помогает в работе с переменными и формулами.
Геометрия изучает фигуры, пространство и их свойства. Знание геометрии позволяет визуализировать данные и создавать графики, а также работать с координатами и расстояниями.
Теория чисел и дискретная математика используются для работы с целыми числами, последовательностями и структурами данных. Они помогают в решении задач комбинаторики, алгоритмической оптимизации и криптографии.
Важно отметить, что необходимо также иметь навыки работы с логикой и анализом данных. Логика позволяет строить алгоритмы и проверять их правильность, а анализ данных помогает обрабатывать и интерпретировать информацию.
Знание основ математики для программирования позволяет разработчикам создавать эффективные и надежные программы, решать сложные задачи и развиваться в своей карьере. Поэтому рекомендуется освоить базовые понятия математики и применять их в практической работе.
Основные понятия математики

Основные понятия математики, с которыми полезно ознакомиться, включают:
1. Числа и операции: целые числа, дроби, десятичные дроби, числа с плавающей точкой. Операции, такие как сложение, вычитание, умножение и деление, помогают манипулировать этими числами.
2. Алгебра: понятия, такие как переменные, уравнения и функции, позволяют описывать и решать математические задачи.
3. Геометрия: изучение фигур, отношений между ними, площадей и объемов помогает визуализировать и моделировать объекты в программировании.
4. Тригонометрия: измерение и отношения между углами и сторонами треугольников используются для решения задач, связанных с движением и графиками.
5. Вероятность и статистика: анализ данных, вероятности событий и распределений помогают принимать решения на основе данных и предсказывать результаты.
Понимание основных понятий математики дает программистам возможность анализировать и решать сложные задачи, создавать эффективные программы и разрабатывать алгоритмы с использованием математических операций и концепций.
Необходимым качеством программиста является умение применять математику в программировании и видеть связь между этими двумя областями знаний.
Арифметические операции и их применение в программировании

Арифметические операции включают сложение (+), вычитание (-), умножение (*), деление (/) и остаток от деления (%). Каждая из этих операций имеет свои свойства и применяется в разных ситуациях.
Операция сложения (+) применяется для объединения чисел или числовых значений. Она может быть использована для складывания двух чисел или для конкатенации строк в случае, если один из операндов является строкой.
Операция вычитания (-) используется для вычитания одного числа от другого. Она может быть применена и к целым числам, и к числам с плавающей запятой.
Операция умножения (*) служит для умножения двух чисел. Она может применяться как к целым числам, так и к числам с плавающей запятой.
Операция деления (/) выполняет деление одного числа на другое. Результатом является число с плавающей запятой. Операция также может применяться и к целым числам, но в этом случае результат будет округлен до целого.
Операция остатка от деления (%) используется для получения остатка от деления одного числа на другое. Например, 5 % 2 равно 1, так как при делении 5 на 2 получается остаток 1.
В программировании арифметические операции могут быть использованы для решения различных задач. Например, они могут быть использованы для подсчета суммы товаров в корзине интернет-магазина, для вычисления среднего значения числового массива или для выполнения математических операций в сложных алгоритмах.
Понимание основных арифметических операций и их применение в программировании является важным для разработчиков, так как они позволяют выполнять математические вычисления и решать различные задачи эффективно.
Работа с переменными и выражениями
Выражение представляет собой комбинацию операндов и операций, которая вычисляется в определенное значение. Операндами могут быть литералы, переменные или другие выражения, а операции выполняют заданные действия над операндами. Результат вычисления выражения может быть присвоен переменной или использован в дальнейших вычислениях.
Для работы с переменными и выражениями существуют различные операторы, позволяющие выполнять различные операции. Например, оператор присваивания (=) используется для присвоения значения переменной, арифметические операторы (+, -, *, /) позволяют выполнять арифметические операции над числами.
Правильное использование переменных и выражений является важным аспектом программирования. Неправильное объявление переменных или ошибки в выражениях могут привести к непредсказуемому поведению программы или ошибкам во время выполнения. Поэтому важно иметь хорошее понимание основ математики и уметь правильно работать с переменными и выражениями.
Логические операции и их использование в программировании
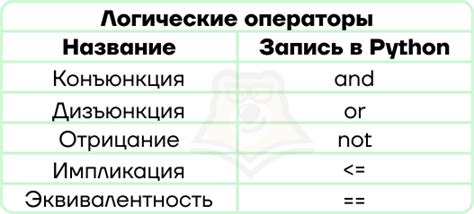
Существуют три основные логические операции:
- Операция «И» (AND) - возвращает истинное значение, только если оба операнда истинны. Если хотя бы один операнд ложный, то результат будет ложным.
- Операция «ИЛИ» (OR) - возвращает истинное значение, если хотя бы один из операндов истинный. Если оба операнда ложные, то результат будет ложным.
- Операция «НЕ» (NOT) - возвращает значение, противоположное операнду. Если операнд истинный, то результат будет ложным, и наоборот.
Логические операции широко применяются при работе с условными выражениями и циклами. Например, для проверки условий, сравнения значений или выполнения различных ветвей программы в зависимости от условий. Также они могут использоваться для комбинирования нескольких условий в одном выражении.
Программирование без знания и понимания логических операций было бы очень сложным, так как они позволяют создавать более гибкие и эффективные программы. Поэтому важно хорошо освоить их использование и правильно применять в своих проектах.
Работа с условиями и циклами
Условные операторы позволяют выполнять определенный блок кода только при выполнении определенного условия. Самым простым и распространенным условным оператором является оператор if. Он позволяет провести проверку условия и выполнить определенный блок кода, только если условие истинно. Кроме оператора if, существуют также операторы else и else if, которые позволяют задать альтернативные условия.
Циклы позволяют выполнять повторяющиеся операции определенное количество раз или до тех пор, пока выполняется определенное условие. Наиболее часто используемыми циклами являются циклы while и for. Цикл while выполняет определенный блок кода до тех пор, пока заданное условие истинно. Цикл for используется для выполнения определенного количества повторений, о котором заранее известно, или для перебора элементов в массиве или коллекции.
Комбинируя условные операторы и циклы, можно создавать более сложные программы, в которых данные обрабатываются их зависимости от различных условий. Знание основ математики позволяет более легко строить логику работы программы и эффективно использовать условия и циклы.
Применение математики в алгоритмах и структурах данных

Одно из ключевых применений математики в алгоритмах и структурах данных - это анализ времени выполнения алгоритмов. Здесь на помощь приходят знания о функциях и их свойствах. С помощью математического анализа можно определить скорость выполнения алгоритма в худшем, среднем или лучшем случае, а также оценить его эффективность и оптимизировать код. Например, для сортировки массивов важно знать различные алгоритмы сортировки и их временную сложность в зависимости от размера входных данных.
Другое важное применение математики в алгоритмах и структурах данных - это работа с числами и числовыми операциями. Здесь математические концепции позволяют разработчикам выполнять сложные вычисления и операции с числами, такие как поиск наибольшего общего делителя, определение простоты числа или решение линейных уравнений.
Также математика используется при создании и анализе различных структур данных, таких как графы, деревья и хеш-таблицы. Знание теории графов позволяет эффективно работать с графовыми алгоритмами, такими как поиск кратчайшего пути или поиск цикла. Алгоритмы на деревьях также могут использовать математические концепции, такие как бинарные поисковые деревья или красно-черные деревья, чтобы обеспечить оптимальное хранение и поиск данных.
В конечном итоге, понимание и применение математики в алгоритмах и структурах данных позволяет программистам создавать эффективные и оптимизированные решения для различных задач. Изучение базовых математических принципов, таких как алгебра, дискретная математика и теория вероятностей, позволяет развивать навыки анализа и решения проблем, а также сделать программирование более эффективным и мощным инструментом.



