Знания математики и умение правильно выполнять математические операции - важные навыки, которые помогают нам во многих аспектах нашей жизни. Одним из важных вопросов, связанных с математикой, является определение порядка выполнения операций. В частности, многие люди задаются вопросом о том, что сначала следует выполнять - деление или умножение, когда они встречаются в выражениях.
Чтобы понять правильный порядок действий, нужно знать о том, что в математике существует определенная система приоритетов для выполнения операций. Эта система называется "порядок действий" или "приоритет операций". Она позволяет нам определить, какие операции следует выполнять первыми, а какие - последними.
В порядке действий первым приоритетом обладает группа операций, которые выполняются перед всеми остальными. Это операции в скобках и операции с высоким приоритетом, такие как возведение в степень и извлечение корня. После них следуют операции умножения и деления, а затем операции сложения и вычитания.
Таким образом, ответ на вопрос "что сначала - деление или умножение?" - зависит от того, в какой последовательности они встречаются в выражении. Если умножение и деление находятся рядом друг с другом без скобок, то выполняется операция, которая указана первой слева направо. Если в выражении присутствуют скобки, то сначала выполняются операции внутри скобок, а затем уже операции снаружи скобок.
Основы математики и порядок действий

Один из основных принципов математики - порядок действий, или, как его называют, приоритет операций. В математических выражениях с несколькими операциями нужно выполнять действия в определенном порядке, чтобы получить правильный ответ.
Начиная с простейших действий – сложения и вычитания, можно двигаться дальше к делению и умножению. Но как определить, с чего начать - деление или умножение?
Существует общепринятый порядок действий, который помогает упорядочить математические операции. Согласно ему, сначала выполняются операции в скобках, затем деление и умножение, а потом сложение и вычитание. Этот порядок называется Приоритетом операций.
Таким образом, если в выражении нет скобок, сначала выполняются операции деления, а потом умножения. Например, в выражении 6 ÷ 2 × 3 = 3 × 3 = 9. Сначала мы выполняем деление 6 ÷ 2 = 3, а затем умножение 3 × 3 = 9.
Исключение из этого правила составляют ситуации, когда в выражении есть операции с одинаковым приоритетом. В таких случаях операции выполняются слева направо. Например, в выражении 4 + 2 - 1, сначала выполняется сложение 4 + 2 = 6, а затем вычитание 6 - 1 = 5.
Что сначала - деление или умножение?
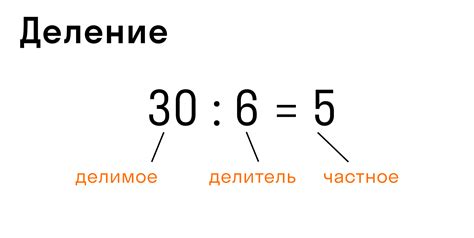
Согласно порядку действий, сначала выполняется умножение, а затем – деление. Это правило следует использовать в случаях, когда умножение и деление находятся в одном выражении, без скобок и других операций.
Например, если у нас есть выражение 6 × 3 ÷ 2, сначала мы должны выполнить умножение 6 × 3, получая 18. Затем, уже зная результат умножения, мы выполняем деление 18 ÷ 2 и получаем ответ 9.
Однако, если у нас есть выражение с использованием скобок, то внутри скобок мы всегда выполняем операции в первую очередь. Например, в выражении (6 × 3) ÷ 2, мы должны сначала выполнить умножение в скобках, получая 18, и только затем выполнять деление на 2, получая 9.
Помните, что использование правильного порядка действий в математике очень важно, чтобы получить корректный результат. Соблюдение порядка действий обеспечивает однозначность и точность в решении математических задач.
Порядок действий в математике

Порядок действий в математике определяется правилом PEMDAS, которое ставит определенные операции в приоритетном порядке. PEMDAS расшифровывается следующим образом:
- P - скобки (выполнять операции внутри скобок первыми);
- E - вычисление выражений с экспонентами (возведение в степень);
- M - умножение;
- D - деление;
- A - сложение;
- S - вычитание.
При выполнении математических операций нужно придерживаться данного порядка. Например, при наличии сложения, вычитания, умножения и деления в выражении, сначала выполняются операции, связанные с умножением и делением, а затем сложение и вычитание.
В случае, если в выражении присутствуют скобки, необходимо выполнить операции внутри скобок первыми. Это помогает сохранить правильный порядок действий и получить правильный результат. Если внутри скобок есть еще одна скобка, то операции во внутренней скобке выполняются первыми.
Значение правильно выполненных операций определяется в соответствии с правилами математики. При неправильном порядке действий можно получить неверный результат, что может повлиять на правильность решения задачи или расчетов.
Какие правила следовать при выполнении математических операций?
При выполнении математических операций необходимо придерживаться определенных правил, чтобы получить правильный результат. Вот основные правила, которые следует соблюдать:
| Операция | Правила |
|---|---|
| Сложение |
|
| Вычитание |
|
| Умножение |
|
| Деление |
|
Следуя этим правилам, можно точно и надежно выполнять математические операции и получать корректные результаты.
Принципы порядка действий в математике

В математике существуют определенные правила, которые помогают определить порядок выполнения операций. Эти правила, также называемые порядком действий, обеспечивают единообразие и точность в вычислениях.
| Операция | Порядок выполнения |
|---|---|
| Скобки | Выполняются первыми |
| Степень | Выполняется второй |
| Умножение и деление | Выполняются в третью очередь |
| Сложение и вычитание | Выполняются последними |
Применение этих правил позволяет достичь правильных ответов при выполнении математических выражений. При отсутствии скобок, степеней или других операций, порядок выполнения основан на так называемом "левостороннем" приоритете, где умножение и деление имеют больший приоритет перед сложением и вычитанием.
Нарушение порядка действий может привести к неверному результату. Поэтому важно запомнить и правильно применять эти принципы, чтобы успешно решать задачи и вычислять значения выражений.
Значение последовательности операций в математике

Порядок действий в математике определяется стандартным правилом: сначала выполняется умножение и деление, а затем сложение и вычитание. Это правило известно как система приоритетов или операторный приоритет.
Например, представьте выражение: 4 * 2 + 6. Согласно системе приоритетов, сначала нужно выполнить умножение (4 * 2 = 8), а затем сложение (8 + 6 = 14), получив итоговый ответ 14.
Если не соблюдать порядок действий, результат может быть неверным. Чтобы избежать ошибок, всегда помните о системе приоритетов и выполняйте операции в правильной последовательности.
Однако существуют случаи, когда порядок действий может быть изменен, используя скобки. Скобки позволяют группировать операции и указывать, какие действия должны быть выполнены первыми. Они имеют самый высокий приоритет в системе приоритетов. Например, в выражении: 4 * (2 + 6), сначала выполняется сложение (2 + 6 = 8), затем умножение (4 * 8 = 32), получив итоговый ответ 32.
Следование системе приоритетов и правильная последовательность операций позволяют достичь верных результатов в математике. Знание и понимание этого правила является фундаментальным для научного подхода к решению задач и применению математических концепций в реальной жизни.



