Алгебра – одна из основных математических дисциплин, изучение которой начинается еще в младших классах. Однако, только восьмиклассники максимально углубляются в ее изучение и получают более серьезные знания и навыки. Восьмой класс – это время, когда ученики начинают изучать такие важные темы, как алгебраические уравнения, факторизация, рациональные числа и многое другое.
Восьмиклассники проходят прописывание и решение различных алгебраических уравнений, начиная с простых линейных и доходя до квадратных. Они учатся переносить члены уравнений из одной части в другую, пытаясь найти неизвестные величины. Это помогает развивать логическое мышление и аналитические навыки.
Важной частью программы алгебры в восьмом классе является изучение факторизации. Ученики узнают, как разложить алгебраические выражения на простые множители и сократить их. Это помогает им более эффективно работать с алгебраическими уравнениями и выражениями в дальнейшем. Процесс факторизации также развивает логику и творческое мышление у школьников.
Помимо этого, они изучают рациональные числа и основные операции с ними. Учатся складывать, вычитать, умножать и делить дроби, а также преобразовывать их в десятичные дроби и наоборот. Эти знания и навыки позволяют ученикам успешно решать задачи, связанные с реальными ситуациями, а также облегчают дальнейшее изучение алгебры в старших классах.
Что изучают школьники в восьмом классе в программе алгебры

Восьмой класс является важным этапом в изучении алгебры, так как здесь школьники начинают более серьезно знакомиться с алгебраическими выражениями, уравнениями и системами уравнений.
В рамках программы алгебры в восьмом классе школьники изучают следующие темы:
- Алгебраические выражения. Восьмиклассники изучают как упрощать и раскрывать скобки в алгебраических выражениях, а также как сокращать дроби и производить действия с ними.
- Уравнения и неравенства. Восьмой класс наполнен изучением различных типов уравнений и неравенств, таких как линейные, квадратные, степенные, рациональные и тригонометрические. Школьники также изучают методы решения этих уравнений и неравенств.
- Системы уравнений. Восьмиклассники учатся решать системы линейных и квадратных уравнений с двумя и тремя переменными, используя различные методы.
- Прикладные задачи. В рамках программы школьники решают различные прикладные задачи, которые помогают им применить полученные знания в реальных ситуациях.
Изучение алгебры в восьмом классе не только развивает логическое мышление и математическую грамотность, но и является важной основой для изучения более сложных тем в старших классах и вузе. Поэтому восьмиклассники должны усвоить все основные понятия и методы алгебры, чтобы успешно продолжить свое образование.
Основы алгебры восьмого класса

Основные темы алгебры восьмого класса включают в себя:
| Тема | Описание |
|---|---|
| Алгебраические выражения | Изучение основных операций с алгебраическими выражениями, включая сложение, вычитание, умножение и деление. Различные методы сокращения и упрощения алгебраических выражений. |
| Уравнения и неравенства | Изучение методов решения уравнений и неравенств с одной и двумя переменными. Решение систем уравнений и неравенств. Применение полученных навыков для решения практических задач. |
| Графики | Определение, построение и анализ графиков линейных и квадратичных функций. Изучение свойств графиков и их влияния на решение уравнений и неравенств. |
| Степени и корни | Работа с понятиями степеней и корней. Изучение операций со степенями и корнями, а также их применение для решения уравнений. |
| Пропорции и пропорциональные отношения | Разбор концепции пропорции и пропорциональных отношений. Решение задач на пропорции и их применение в реальных ситуациях. |
Изучение этих основ алгебры позволяет школьникам углубить свои знания и навыки в математике, а также подготовиться к изучению более продвинутых тем в старших классах.
Решение уравнений и неравенств
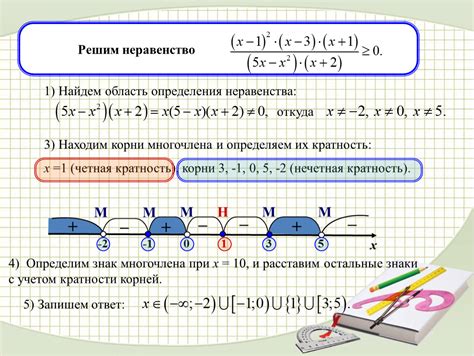
Неравенства тоже имеют важное значение в алгебре. Ученики узнают, как решать линейные и квадратные неравенства, используя методы, подобные решению уравнений. Они учатся определять интервалы, в которых выполняются неравенства и решать комплексные неравенства с использованием систем неравенств.
При изучении решения уравнений и неравенств ученики также узнают о графическом представлении уравнений и неравенств на координатной плоскости. Они изучают графики функций и учатся находить точки пересечения графиков с осями координат для определения решений уравнений и неравенств.
Изучение решения уравнений и неравенств восьмым классом является важным шагом в математическом образовании школьников. Эти навыки будут полезными в дальнейшем изучении алгебры и других математических дисциплин.
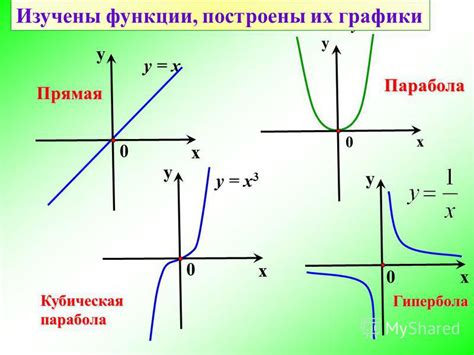
Функции и графики в алгебре
Важными понятиями в изучении функций являются область определения и область значений. Область определения функции - это множество всех значений аргумента, при которых функция существует и имеет значение. Область значений функции - это множество всех значений функции, которые она может принимать. Часто область значений представляется в виде интервала или множества.
Школьники учатся строить графики функций на координатной плоскости. Для этого используются различные методы, включая построение таблицы значений, изучение поведения функции на разных участках области определения, а также определение и анализ поведения функции в окрестности точек разрыва и особых точек.
График функции может иметь различные формы, такие как ступенчатый, линейный, параболический, гиперболический и т.д. Школьники учатся распознавать эти формы и анализировать характеристики графиков, такие как наклон, симметрия, экстремумы, разрывы и асимптоты.
| Форма графика | Описание |
|---|---|
| Ступенчатый | График функции состоит из прямых участков, соединенных вертикальными или горизонтальными линиями. |
| Линейный | График функции представляет собой прямую линию. |
| Параболический | График функции имеет форму параболы. |
| Гиперболический | График функции имеет форму гиперболы. |
Системы линейных уравнений

Системы линейных уравнений представляют собой наборы уравнений, в которых неизвестные переменные связаны между собой линейными зависимостями. В восьмом классе школьники изучают работу с системами линейных уравнений с двумя и тремя неизвестными, применяя методы решения, такие как метод подстановки, метод равенства коэффициентов и метод графического представления.
Для решения систем линейных уравнений необходимо преобразовать их в однородную или неоднородную форму и применить соответствующие методы решения. Метод подстановки заключается в выражении одной переменной через другую и последующей подстановке полученного выражения в остальные уравнения системы. Метод равенства коэффициентов позволяет найти значения неизвестных путем приравнивания соответствующих коэффициентов. Метод графического представления основан на построении графиков уравнений системы и нахождении их точек пересечения.
Изучение систем линейных уравнений важно для школьников, так как они широко применяются в различных областях науки и техники, а также в повседневной жизни. Решение систем линейных уравнений позволяет находить значения неизвестных в различных задачах, например, при составлении расписания, оптимизации процессов в производстве и т.д. Понимание основных методов решения систем линейных уравнений помогает школьникам развивать аналитическое мышление и навыки работы с алгебраическими выражениями.



