Основной закон динамики вращательного движения формулируется в рамках механики и определяет отношение между силой, моментом силы и угловым ускорением тела. Этот закон является аналогом основного закона динамики поступательного движения, но применяется к вращению твердого тела вокруг оси.
Основным законом динамики вращательного движения является формула:
М = I ● α
где М - момент силы, действующей на тело, I - момент инерции тела, α - угловое ускорение тела. Данная формула позволяет определить, какое угловое ускорение возникает под действием определенного момента силы и какой момент силы требуется для достижения заданного углового ускорения.
Основной закон динамики вращательного движения имеет важное значение при решении задач в механике. Он позволяет описывать и прогнозировать движение вращающихся тел, определять условия равновесия и устойчивости системы, а также эффективно управлять процессом вращения. Понимание этого закона позволяет более глубоко изучать принципы работы вращающихся механизмов и разрабатывать эффективные конструкции для различных технических устройств.
Определение вращательного движения
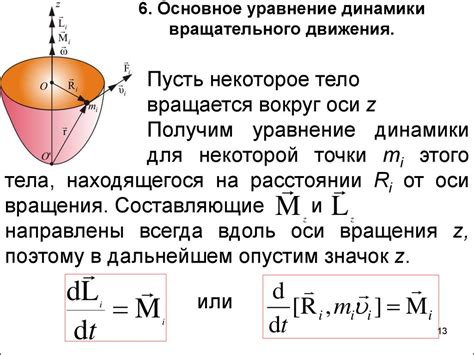
Основной закон динамики вращательного движения, или закон сохранения момента импульса, гласит, что если на тело не действуют моменты сил, то момент импульса этого тела остается постоянным.
Момент импульса тела определяется как произведение массы тела на его угловую скорость и момент инерции тела относительно оси вращения. Момент инерции зависит от формы и распределения массы тела относительно оси вращения.
Вращательное движение широко применяется в различных областях науки и техники. Оно является основой для работы механизмов, таких как колеса, роторы, шестерни и другие устройства.
Основной закон динамики вращательного движения

Момент импульса – это векторная величина, которая определяется как произведение массы тела на его скорость и радиус-вектор относительно оси вращения. При изменении радиус-вектора или скорости тела, изменяется и его момент импульса.
Закон сохранения момента импульса применяется для изучения различных явлений, связанных с вращательным движением, таких как вращение твердого тела, движение волчка, полеты спутников и т. д.
Важно отметить, что закон сохранения момента импульса действует только в том случае, когда на систему тел не действуют внешние вращательные моменты. Если же на систему действуют внешние моменты сил, то момент импульса системы будет изменяться.
Приложение основного закона к вращательным системам
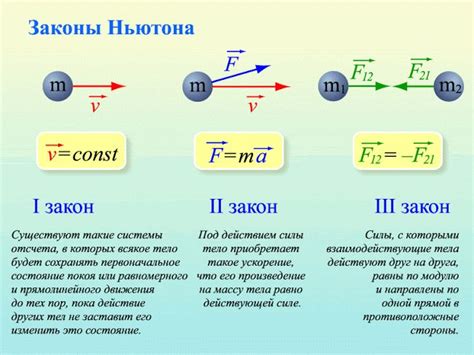
Основной закон динамики вращательного движения утверждает, что момент силы, действующей на вращающееся тело, равен произведению момента инерции тела на его угловое ускорение. Этот закон может быть применен к различным вращательным системам, таким как вращающиеся диски, колеса, оси вращения и т. д.
Одним из примеров применения основного закона динамики вращательного движения является расчет момента инерции и углового ускорения вращающегося диска. Для этого нужно знать массу диска, его радиус и скорость вращения. Момент инерции диска рассчитывается с помощью формулы: I = ½ * m * r², где m - масса диска, r - радиус диска. Угловое ускорение определяется как отношение изменения угловой скорости к изменению времени.
Другим примером применения закона динамики вращательного движения является расчет момента силы, действующей на вращающееся колесо. Если на колесо действует внешняя сила (например, сила трения), то можно рассчитать момент этой силы вращения. Формула для расчета момента силы: M = F * r, где F - сила, действующая на колесо, r - радиус колеса. Угловое ускорение колеса также может быть рассчитано, используя формулу из основного закона динамики вращательного движения.
Использование основного закона динамики вращательного движения позволяет рассчитать различные параметры вращательных систем и предсказать их поведение при воздействии сил. Это имеет практическое применение в различных областях, таких как машиностроение, физика, робототехника и другие.
| Примеры вращательных систем | Формула для расчета момента инерции | Формула для расчета момента силы |
|---|---|---|
| Диск | I = ½ * m * r² | M = F * r |
| Колесо | I = ½ * m * r² | M = F * r |
| Ось вращения | I = ½ * m * r² | M = F * r |
Основной закон динамики вращательного движения утверждает, что изменение момента импульса вращающегося тела равно моменту внешнего вращательного момента силы, приложенной к этому телу.
1. Вращательное движение имеет момент инерции.
Момент инерции является аналогом массы в вращательном движении. Он характеризует инертность тела относительно оси вращения. Чем больше момент инерции, тем тяжелее изменить скорость вращения тела.
2. Момент силы равен произведению момента инерции на угловое ускорение.
Момент силы, также называемый вращательным моментом, зависит от силы, её приложения к телу и расстояния до оси вращения. Чем больше момент силы, тем больше угловое ускорение тела.
3. Момент импульса сохраняется во времени.
По закону сохранения момента импульса, если на тело не действуют внешние моменты сил, то его момент импульса остается постоянным. Таким образом, вращающееся тело сохраняет свою угловую скорость и не изменяет направление вращения.
Взаимодействие сил в вращательной системе

Основной закон динамики вращательного движения гласит, что вращательное движение тела возникает под действием момента силы, равного произведению массы тела на угловое ускорение.
Взаимодействие сил в вращательной системе может быть достаточно сложным и включать различные виды сил. Для правильного изучения вращательного движения необходимо учитывать все силы, действующие на тело. Некоторые из основных сил, влияющих на вращательное движение, включают:
- Силы инерции – возникают в результате вращения тела и стремятся сохранить его угловую скорость и направление.
- Силы трения – могут противодействовать вращению тела и вызывать его заторможение.
- Силы внешних воздействий – действуют на тело со стороны окружающей среды и могут включать силы тяжести, сопротивления среды и другие воздействующие силы.
Взаимодействие сил в вращательной системе может определять характер вращательного движения тела и его устойчивость. Правильное понимание и учет всех сил, действующих в системе, позволяет предсказать и объяснить поведение тела при вращении, а также рассчитать его параметры и характеристики.
Равнодействующая вращательных сил
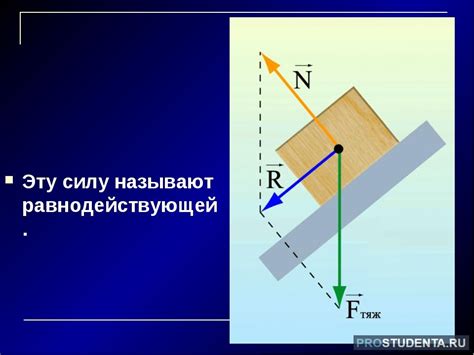
Равнодействующая вращательных сил – это сумма всех моментов сил, приложенных к телу, и обладающая следующими характеристиками:
- Величина равна алгебраической сумме моментов сил.
- Направление определяется правилом правой руки и зависит от направления каждого момента сил.
Для нахождения равнодействующей вращательных сил необходимо рассмотреть все моменты сил, действующих на тело, и просуммировать их алгебраически.
Сумма моментов сил, приложенных к телу, равна произведению силы F на плечо r, то есть:
| Момент силы | F | r |
|---|---|---|
| M | F1 | r1 |
| M | F2 | r2 |
| ... | ... | ... |
Таким образом, равнодействующая вращательных сил вычисляется путем сложения всех моментов сил, действующих на тело.
Практическое применение основного закона вращательного движения
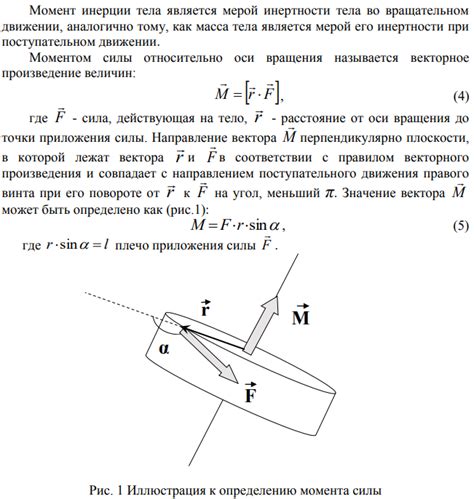
Основной закон динамики вращательного движения, также известный как второй закон Ньютона для вращательного движения, играет важную роль в решении практических задач, связанных с вращающимися объектами.
Один из примеров практического применения этого закона - расчет момента инерции. Момент инерции является важной характеристикой вращательного движения и определяет его инерцию относительно оси вращения. Для разных физических объектов момент инерции вычисляется с использованием основного закона вращательного движения.
Еще одним примером применения этого закона может быть определение углового ускорения тела. Угловое ускорение является мерой изменения скорости вращения объекта, а его величина может быть определена с использованием основного закона вращательного движения.
Кроме того, основной закон вращательного движения применяется для расчета момента силы и углового момента. Момент силы определяет вращательный эффект, создаваемый силой, действующей на объект, а угловой момент является мерой вращательного эффекта, вызываемого приложенной силой.
Общая формула основного закона вращательного движения выражается как:
Момент силы = Момент инерции × Угловое ускорение
Таким образом, практическое применение основного закона вращательного движения помогает в решении различных задач, связанных с вращающимися объектами, и является важным инструментом для анализа и предсказания их поведения.



