Логарифмы - это математическая операция, которая позволяет нам решать различные задачи на практике, особенно в физике, экономике и информатике. Иногда нам может потребоваться возвести логарифм в квадрат. Однако, данная задача может показаться сложной, особенно для тех, кто только начинает изучать математику.
В данной статье мы предлагаем вам несколько полезных советов о том, что делать при возведении логарифма в квадрат. Во-первых, необходимо знать основные свойства логарифмов. Например, можно воспользоваться свойствами логарифмов для упрощения выражения. Кроме того, существует специальная формула для возведения натурального логарифма в квадрат.
Если вы столкнулись с задачей, которая требует возведения логарифма в квадрат, не волнуйтесь. Возможно, вы уже знаете, что делать, но вам не хватает уверенности. В данной статье мы приведем примеры различных задач, где необходимо возвести логарифм в квадрат, и подробно распишем процесс их решения.
Что делать при возведении логарифма в квадрат? Полезные советы
1. Используйте свойства логарифмов. Они помогут вам упростить задачу при возведении логарифма в квадрат. Например, если у вас есть логарифм суммы двух чисел, то его можно разбить на два отдельных логарифма, что значительно упростит решение.
2. Постепенно продвигайтесь вперед. Если вам задано выражение, в котором нужно возвести логарифм в квадрат, начните с упрощения этого выражения по шагам. Выполните все элементарные операции с логарифмами, раскройте скобки, упростите сложения и вычитания. Постепенно вы придете к итоговому решению.
3. Проверьте ответ. После того, как вы получили итоговое выражение, в котором логарифм возведен в квадрат, проведите обратную операцию и найдите логарифм числа. Убедитесь, что ваш ответ верный, проверив его с помощью калькулятора или другим способом.
4. Закрепите материал. Возведение логарифма в квадрат – это довольно сложная задача, поэтому для ее успешного решения требуется хорошее знание свойств логарифмов. Периодически повторяйте материал и решайте задачи на эту тему, чтобы закрепить свои навыки и быть готовым к сложным заданиям.
Запомните, что возведение логарифма в квадрат – это всего лишь одна из множества математических операций, которые можно выполнять со свойствами логарифмов. Используйте указанные советы, чтобы решать все задачи по этой теме более легко и точно.
Выбор правильной функции
При возведении логарифма в квадрат важно выбрать правильную функцию, чтобы получить корректный результат. В данном случае речь идет о функции возведения в квадрат.
В математике существуют различные функции возведения в квадрат, и важно выбрать ту, которая соответствует задаче. Наиболее распространенными функциями являются:
- Math.pow(x, 2) - эта функция используется во многих программных языках, включая JavaScript. Она принимает два аргумента: число, которое необходимо возвести в квадрат (x), и степень возведения (2). Результатом выполнения этой функции будет число, равное x в квадрате.
- x * x - это простой способ возведения числа x в квадрат. Он основан на свойствах умножения, поскольку квадрат числа можно получить, умножив его само на себя.
При выборе функции возведения логарифма в квадрат рекомендуется обратить внимание на то, как она взаимодействует с другими операциями и какова ее точность. Использование подходящей функции позволит получить результат, отвечающий требованиям задачи.
Определение области определения

При возведении логарифма в квадрат нужно убедиться, что основание логарифма является положительным числом. Если основание отрицательное или равно нулю, то операция возведения логарифма в квадрат не имеет смысла и не определена.
Например, если имеется логарифм с основанием 2, то возведение его в квадрат имеет смысл, так как 2 является положительным числом. Однако, для логарифма с основанием -2 возведение в квадрат не определено и не имеет смысла.
Построение графика
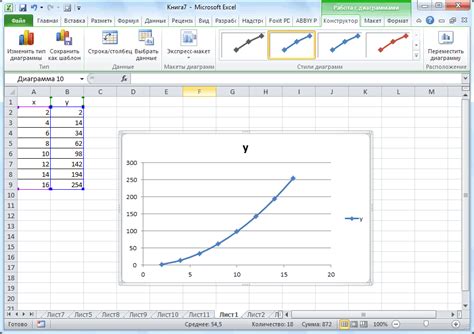
Для построения графика логарифма, возведенного в квадрат, необходимо использовать точки данных, которые соответствуют различным значениям входного аргумента. Для этого можно выбрать несколько значения х и вычислить соответствующие значения у, используя заданную функцию.
Полученные пары координат (х, у) можно использовать для построения графика на плоскости. Ось у будет представлять значение функции, а ось х - значение аргумента. Для более точного представления, можно выбрать больше значений х и построить график, соединяющий все полученные точки.
График функции, полученной путем возведения логарифма в квадрат, может иметь различные формы в зависимости от базы логарифма и коэффициента перед логарифмом.
Для наглядного представления графика и удобства анализа его свойств, можно воспользоваться таблицей значений функции на разных интервалах. В таблице строится соответствие между значениями х и у, что позволяет получить представление о взаимной зависимости входного аргумента и значения функции.
| Значение x | Значение y |
|---|---|
| 1 | 0 |
| 2 | 0.693 |
| 3 | 1.386 |
| 4 | 1.099 |
| 5 | 1.609 |
| 6 | 1.386 |
По данным значениям x и y можно построить график функции, соединяя полученные точки.
Изучение графика функции, полученной путем возведения логарифма в квадрат, помогает лучше понять ее особенности и поведение. Такой анализ может быть полезен при решении задач и принятии решений в различных областях науки и техники.
Решение уравнений

При возведении логарифма в квадрат в уравнении, необходимо следовать определенным шагам для его решения.
- Перепишите уравнение в экспоненциальной форме.
- Уберите логарифм, применяя принцип эквивалентных преобразований.
- Разрешите уравнение для переменной, выдерживая логарифмические свойства и используя алгебраические методы.
- Проверьте полученное решение, подставив его обратно в исходное уравнение.
Решая уравнение с возведением логарифма в квадрат таким образом, можно получить точное решение. Важно помнить использовать правильные математические приемы и проверять полученные ответы. Удачного решения ваших уравнений!
Применение в реальной жизни

1. Финансы и инвестиции:
Логарифмические модели используются для анализа финансовых рынков и прогнозирования цен на финансовые инструменты. Возведение логарифма в квадрат может упростить расчеты и улучшить прогнозирование процентных ставок, изменений цен акций и других финансовых показателей.
2. Статистика и эксперименты:
Логарифмическое преобразование может применяться для обработки и анализа данных, особенно тех, которые имеют широкий диапазон значений или неоднородное распределение. Возведение логарифма в квадрат помогает сгладить экстремальные значения и улучшить интерпретацию результатов.
3. Инженерия и наука:
Логарифмические шкалы широко используются в инженерии и науке для измерения и представления величин различных физических параметров. Возведение логарифма в квадрат позволяет лучше визуализировать данные, повышает точность и упрощает анализ этих величин.
4. Технологии и информатика:
Метод возведения логарифма в квадрат применяется в некоторых алгоритмах и программных системах для обработки данных, сжатия информации и улучшения качества сигналов. Это может быть полезно в области аудио- и видеообработки, обработки изображений, сжатия файлов и других технологических процессов.
Таким образом, возведение логарифма в квадрат имеет широкий спектр применений в реальной жизни и играет важную роль в различных областях науки, техники, финансов, статистики и других дисциплин.



