Математика – это наука, основанная на строгой логике и законах. Однако, время от времени, мы можем столкнуться с ситуацией, когда под корнем оказывается отрицательное число. Это вызывает беспокойство и неоднозначность, поскольку обычно мы привыкли работать только с положительными числами. Но не стоит паниковать! В данной статье мы рассмотрим несколько способов решения этой проблемы и попытаемся разобраться, что делать, когда мы сталкиваемся с корнем отрицательной степени.
Первым и наиболее распространенным способом решения проблемы корня отрицательной степени является введение комплексных чисел. Комплексные числа – это особый класс чисел, который включает в себя мнимую единицу √-1, обозначаемую символом i. В комплексной алгебре, корни отрицательной степени можно представить в виде комплексных чисел. Например, корень квадратный из -1 равен имениной единице i. И, хотя поначалу концепция комплексных чисел может показаться сложной, они играют важную роль в математике и имеют множество применений в реальной жизни, включая электротехнику и физику.
Если введение комплексных чисел кажется слишком сложным или излишне для вашей текущей задачи, существует также другой способ решения этой проблемы. Он основан на использовании тригонометрических функций. Вы можете применить формулу Эйлера, которая связывает тригонометрические функции с комплексными числами. С помощью этой формулы вы можете выразить корень отрицательной степени через синус и косинус требуемого угла. Этот метод, хотя и требует некоторых математических знаний, может быть более простым и интуитивным для решения задачи, чем введение комплексных чисел.
Как исправить отрицательную степень под корнем

Отрицательная степень под корнем возникает, когда мы пытаемся извлечь корень из отрицательного числа. В таких случаях можно применить несколько методов для исправления этой ситуации.
1. Введение комплексных чисел. В математике существует понятие комплексных чисел, которые позволяют извлекать корни из отрицательных чисел. Если вы знаете, что работаете с комплексными числами, можно использовать специальные формулы для получения корня.
2. Использование модуля числа. Модуль числа - это его абсолютная величина, то есть число без его знака. Если вы сталкиваетесь с отрицательной степенью под корнем, вы можете взять модуль этого числа и затем вычислить корень из него. Но помните, что результат будет комплексным числом.
3. Проверка наличия вещественного корня. Иногда отрицательная степень под корнем может быть ошибкой, вызванной неверными входными данными или некорректными расчетами. Перед тем, как искать способы исправления отрицательной степени, проверьте, возможно ли вообще извлечь вещественный корень из этого числа.
Всегда будьте внимательны и обращайте внимание на результаты своих вычислений. Если вы столкнулись с отрицательной степенью под корнем, примените один из приведенных методов, чтобы исправить ошибку и продолжить свои расчеты.
Шаг 1: Возведение в степень с положительным показателем

Перед тем как рассматривать, что делать, если под корнем отрицательная степень, давайте вспомним, как возводить число в положительную степень. Если у нас есть число a и положительное число n, то мы можем возвести число a в степень n следующим образом:
1. Умножаем число a на само себя n раз.
2. Получаем результат, который является произведением n множителей, равных числу a.
В математической нотации это можно записать следующим образом:
an = a × a × a × ... × a (n раз)
Зная эту основу, мы можем перейти к обсуждению, что делать, если нам дано число, которое нужно возвести в отрицательную степень.
Шаг 2: Использование дробей для представления отрицательной степени
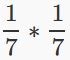
Если под корнем находится отрицательная степень, то можно использовать дроби для ее представления. Для этого нужно превратить отрицательную степень в положительную, а затем использовать дробь.
Процедура следующая:
- Найдите модуль отрицательной степени.
- Превратите отрицательную степень в положительную, взяв обратное значение.
- Используйте полученное положительное значение в качестве степени и примените его к числу под корнем.
- Если показатель степени после превращения отрицательной степени в положительную равен 1, то под корнем будет дробь.
Например, если у нас есть корень кубический из (-27), то сначала превратим отрицательную степень в положительную:
|-3| = 3
Затем используем полученное положительное значение в качестве степени и применяем его к числу под корнем:
∛(27) = 3
В итоге получаем корень кубический из (-27) равным -3.
Поэтому, если под корнем находится отрицательная степень, можно использовать дробь для ее представления, применяя указанную процедуру.
Шаг 3: Применение комплексных чисел для отрицательных степеней

Как мы уже узнали в предыдущих шагах, под корнем отрицательной степени не существует реального числа. Однако, в математике мы можем ввести понятие комплексных чисел, которые дают нам возможность работать с такими степенями.
Для вычисления отрицательной степени числа, нам необходимо сначала представить число в виде комплексного числа. Комплексное число состоит из действительной и мнимой частей, обозначаемых как a и b соответственно, и записывается в виде a + bi, где i - мнимая единица, такая что i² = -1.
Представим число в виде комплексного числа: x = a + bi, где a и b - действительные числа, а i - мнимая единица. Затем возводим его в отрицательную степень n: x⁻ⁿ = (a + bi)⁻ⁿ.
Для вычисления отрицательной степени комплексного числа используется формула Де Муавра:
| Формула Де Муавра | Формула для вычисления отрицательной степени |
|---|---|
| (a + bi)ⁿ = rⁿ * (cos(nθ) + isin(nθ)) | (a + bi)⁻ⁿ = 1 / (rⁿ * (cos(nθ) + isin(nθ))) |
Здесь r - модуль числа (расстояние от нуля до точки на комплексной плоскости, вычисляемое по формуле r = sqrt(a² + b²)), а θ - аргумент числа (угол между положительным направлением оси x и линией, соединяющей начало координат и точку на комплексной плоскости, вычисляемый по формуле θ = arctan(b / a)).
Итак, чтобы найти отрицательную степень комплексного числа, мы сначала вычисляем его модуль и аргумент, затем подставляем полученные значения в формулу Де Муавра. После этого у нас получится выражение вида 1 / (rⁿ * (cos(nθ) + isin(nθ))), которое можно упростить и вычислить.
Таким образом, применение комплексных чисел позволяет нам работать с отрицательными степенями, которые невозможно представить в виде реальных чисел.
Шаг 4: Упрощение выражений с отрицательной степенью под корнем

При решении задач, где под корнем находится отрицательная степень, мы можем воспользоваться следующими правилами упрощения выражений:
1. Корень отрицательного числа. Если под корнем находится отрицательное число, то решение задачи невозможно в области вещественных чисел. В этом случае необходимо перейти к области комплексных чисел и использовать формулу для вычисления корней комплексных чисел. Результатом таких вычислений будет комплексное число.
2. Применение свойств степеней. Если под корнем находится отрицательная степень, мы можем воспользоваться свойством степени и переписать выражение в виде обычной дроби с положительным показателем степени. Например, √(x^(-n)) = 1/√(x^n).
Применение этих правил позволяет нам более гибко и эффективно решать задачи с отрицательными степенями под корнем. Важно помнить, что при использовании комплексных чисел необходимо учитывать их особенности и правила для работы с ними.



