Вопрос о том, что делается первым - плюс или минус, является довольно интересным и часто возникает не только в математике, но и в повседневной жизни.
Один из самых распространенных способов ответить на этот вопрос состоит в использовании правила знаков. Согласно этому правилу, плюс всегда ставится перед числом, а минус - перед знаком числа.
Например, если мы хотим вычесть отрицательное число из положительного, то мы можем записать это как 3 - (-2), где минус перед числом -2 указывает на то, что это отрицательное число. В этом случае плюс стоит перед числом 3 и мы получаем результат 5.
Что делается вначале - плюс или минус?
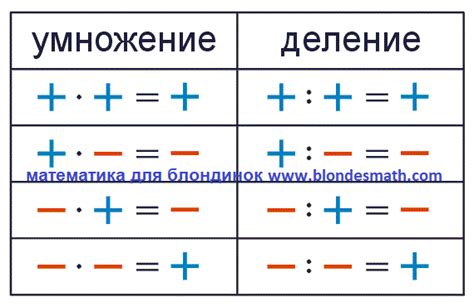
При выполнении математических операций, в том числе сложения и вычитания, плюс всегда выполняется первым. Это связано с правилами математики и логики.
Например, рассмотрим пример: 5 - (-3). Здесь минус перед скобкой означает, что в скобках стоит отрицательное число. Чтобы выполнить данную операцию, необходимо сначала изменить знак числа в скобках на плюс, а затем выполнить вычитание: 5 + 3. Таким образом, плюс выполняется первым.
Также следует отметить, что на практике в математических выражениях часто используются скобки, чтобы явно указать порядок выполнения операций. Например, в выражении 2 * (-4 + 3) + 6 будет сначала выполнено сложение в скобках (-4 + 3), что даст -1, затем умножение (2 * (-1)), что даст -2, и, наконец, сложение (-2 + 6), что даст 4. В данном случае скобки указывают на то, что сначала нужно выполнить операцию внутри них, а затем уже остальные операции.
Каким образом формируются числа

В математике существует определенное соглашение о том, как обозначать знак числа. Знак "+" обозначает положительное число, а знак "-" обозначает отрицательное число. Поэтому, для формирования числа с нужным знаком, необходимо определить его положительное или отрицательное значение.
Расположение цифр в числе также имеет свои правила. В обычной десятичной системе счисления, используется позиционная система. Она основана на том, что значение цифры зависит от ее позиции в числе. Значение цифры в зависимости от ее позиции может быть увеличено или уменьшено в разы.
Например, в числе 567, цифра 5 имеет вес 500, цифра 6 имеет вес 60, а цифра 7 имеет вес 7. В результате формирования числа, каждая цифра вносит свой вклад в итоговое значение числа.
Таким образом, формирование чисел включает определение знака числа и расположение цифр в числе, что позволяет нам получать числовые значения с разными свойствами и особенностями.
Влияние на математические операции

Когда мы имеем дело с числами, то первым делом выполняется операция сложения (знак "плюс"). При сложении двух чисел, результат будет равен их сумме.
Например, если мы прибавим число 5 к числу 3, то получим результат 8:
3 + 5 = 8
Операция вычитания (знак "минус") выполняется после сложения. При вычитании одного числа из другого, результат будет равен разности этих чисел.
Например, если мы вычтем число 3 из числа 8, то получим результат 5:
8 - 3 = 5
Таким образом, порядок выполнения операций "плюс" и "минус" играет важную роль в математических вычислениях. Правильное использование этих операций позволяет получить точный результат.
Порядок появления плюса и минуса

Итак, первым из этой пары символов появился плюс. Он стал применяться вместе с минусом для обозначения положительных и отрицательных чисел. Первое известное употребление символа плюса относится к IV веку, когда греческий математик Диофант использовал его для обозначения положительных чисел.
Минус же появился позднее. Он был введен в математику только к XVI веку и использовался для обозначения отрицательных чисел. Развитие этого символа происходило вместе с развитием алгебры и математического анализа.
Таким образом, порядок появления плюса и минуса определен и исторически обусловлен. Первым стал символ плюса, который начал использоваться еще в Древней Греции, в то время как символ минуса появился значительно позже.
Взаимодействие в физических процессах

Силы могут быть как положительными, так и отрицательными, и они проявляются в различных формах. Силы притяжения, такие как гравитационная или электростатическая, являются примерами положительных сил. Они притягивают объекты друг к другу и способны удерживать их вместе.
Но в физике также существуют и отталкивающие силы, например, магнитное или электростатическое отталкивание. Они проявляются в том, что объекты с одинаковыми зарядами или полярными моментами отталкиваются друг от друга.
Взаимодействие положительных и отрицательных сил играет важную роль во многих физических процессах. Например, в электрических цепях положительные и отрицательные заряды создают разность потенциалов, которая позволяет электрическому току протекать через цепь.
Также положительные и отрицательные заряды взаимодействуют в химических реакциях, где происходят переходы электронов между атомами и молекулами. Это взаимодействие определяет свойства и состав вещества.
Однако во многих физических системах взаимодействие положительных и отрицательных сил может приводить к разрушительным последствиям. Например, при плохом уравновешивании положительной и отрицательной сил в конструкции здания или моста может происходить деформация или разрушение.
Таким образом, взаимодействие положительных и отрицательных сил в физических процессах играет значимую роль и является неотъемлемой частью изучения природы и ее феноменов.
Сокращение в алгебре и арифметике
Первым шагом при сокращении обычно является факторизация числителя и знаменателя выражения или дроби. Это позволяет выявить общие множители, которые можно сократить.
В случае с алгебраическими выражениями, в том числе линейными или квадратичными, можно использовать свойства алгебраических операций, такие как коммутативность, ассоциативность, распределительность и так далее, чтобы упростить выражение.
Сокращение может быть особенно полезным при работе с дробями. Например, при сложении или вычитании дробей часто требуется найти общий знаменатель и сократить дроби до простейшего вида.
Также возможно сокращение отрицательных чисел. Например, если вы имеете две отрицательные дроби или числа и высчитываете их сумму или разность, то оба числа сокращаются по модулю, а знак минуса остается только у результирующего числа.
Итоговая мысль: Сокращение в алгебре и арифметике позволяет упрощать выражения и дроби, делая их более компактными и удобными для дальнейших вычислений. При сокращении следует обратить внимание на общие множители, факторизацию и математические свойства, чтобы достичь простейшего вида выражения или дроби.
Сравнение и эффекты на разных языках

При сравнении операторов плюс и минус на разных языках программирования можно выявить различные эффекты, которые могут повлиять на итоговый результат.
На некоторых языках программирования, например, JavaScript, оператор плюс используется не только для сложения чисел, но и для конкатенации строк. Это означает, что если вы примените оператор плюс к двум строкам, они будут просто склеены в одну строку. В то же время, оператор минус в большинстве языков используется исключительно для математических операций и не имеет такого эффекта на строки.
Также обратите внимание на то, что в разных языках использование оператора плюс или минус может иметь разные приоритеты. Например, в языке PHP оператор плюс имеет более высокий приоритет, чем оператор минус. Это означает, что если вы примените операторы плюс и минус в одном выражении, оператор плюс будет выполнен первым. В других языках, таких как Java или C++, приоритет операторов плюс и минус одинаковый, поэтому порядок выполнения будет зависеть от расположения операторов в выражении.
| Язык программирования | Плюс | Минус |
|---|---|---|
| JavaScript | Конкатенация строк, сложение чисел | Математическое вычитание |
| PHP | Сложение чисел с более высоким приоритетом | Математическое вычитание |
| Java | Сложение чисел с одинаковым приоритетом | Математическое вычитание |
Таким образом, при использовании операторов плюс и минус на разных языках программирования необходимо учитывать их различия в поведении и приоритете, чтобы получить ожидаемый результат.
Роль в жизни и практическом применении

Во-первых, сложение и вычитание применяются в финансовых расчетах. Они позволяют нам управлять своими деньгами, рассчитывать свои расходы и доходы, а также планировать бюджет. Например, если у вас есть определенная сумма денег, вы можете использовать операцию сложения, чтобы узнать, сколько денег у вас будет после добавления новой суммы.
Во-вторых, сложение и вычитание используются в торговле и бизнесе. При покупке товаров или оказании услуги, мы используем операцию сложения, чтобы вычислить общую стоимость. Также, при вычислении налогов и процентов, мы используем операции сложения и вычитания.
Кроме того, сложение и вычитание используются в науке, инженерии и технике. В этих областях операции сложения и вычитания используются для решения уравнений, моделирования и анализа данных.
Сложение и вычитание также важны в повседневной жизни. Они позволяют нам решать простые задачи, такие как подсчет количества предметов или определение времени, в которое нам нужно проснуться, чтобы прийти на работу или в школу.
Таким образом, знание и практическое применение операций сложения и вычитания играет важную роль в различных аспектах нашей жизни, помогая нам в финансовом планировании, бизнесе, науке и ежедневных задачах.



