Число пи - это одна из самых известных констант в математике, обозначаемая греческой буквой π. Оно представляет собой математическую постоянную, которая используется для вычисления длины окружности, площади круга, а также при решении множества других задач.
Число пи является иррациональным, то есть его десятичное представление бесконечно не повторяется и не имеет периода. Оно начинается с 3,14159 и продолжается дальше. Впервые число пи было исследовано еще в Древней Греции, но точное его значение было вычислено только в 20 веке с помощью компьютеров.
Одно из интересных свойств числа пи - его бесконечность. При расчетах и измерениях окружностей и кругов всегда использовалось приближенное значение этой константы, например, 3,14 или 22/7. Однако именно в числе пи находится точное значение, которое невозможно представить в виде конечной десятичной дроби. Это делает число пи особенным и уникальным.
Число пи также является трансцендентным, то есть оно не является решением никакого алгебраического уравнения с рациональными коэффициентами. Это было доказано в середине 19 века математиком Фердинандом Лиувиллем.
Число пи:

Число пи является иррациональным числом, что означает, что его десятичное представление бесконечно длинно и не повторяется. Его значение приближенно равно 3,14159, но точное значение неизвестно.
Число пи имеет множество удивительных свойств и широкий спектр применений. Оно встречается во многих областях науки и техники, таких как физика, математика, инженерия и компьютерные науки.
Некоторые удивительные свойства числа пи:
- Число пи является бесконечным и непериодическим десятичным числом.
- Число пи иррационально, что означает, что его нельзя представить в виде дроби.
- Число пи трансцендентно, что означает, что оно не является решением никакого алгебраического уравнения с рациональными коэффициентами.
- Число пи имеет бесконечное количество десятичных знаков и никогда не повторяется или не раскрывается в некоторую периодическую последовательность.
- Число пи используется для расчета площади и длины окружности, объема и площади шара, и других геометрических параметров.
- Число пи часто встречается в физических формулах, таких как формула для расчета периода колебаний математического маятника.
Число пи является одной из самых известных и удивительных математических констант и продолжает увлекать и вдохновлять ученых и математиков по всему миру.
Определение и происхождение

Первые упоминания числа пи встречаются уже в древнем мире. В древнем Египте и Вавилоне египтяне и вавилонцы использовали приближенные значения π для выполнения геометрических вычислений. Однако первые точные расчеты числа пи были сделаны древнегреческими математиками.
В Индии числом пи начали пользоваться в 5 веке, а уже в 9 веке арабские математики разработали алгоритмы для приближенного нахождения значения числа пи с большей точностью.
На протяжении веков, с появлением новых математических и вычислительных методов, знание о числе пи становилось более точным и точным. С появлением современных компьютеров удалось рассчитать значение π с миллионами знаков после запятой.
Число пи является одной из самых загадочных и мистических математических констант. Оно встречается во многих областях науки и является неисчерпаемым источником увлекательных математических задач и головоломок.
Рациональность или иррациональность

Ученые уже долгое время пытаются найти как можно больше десятичных знаков числа пи, но пока не существует точного значения для него. Тем не менее, математические методы позволяют вычислять его с высокой точностью.
Интересно то, что доказательство иррациональности числа пи было предложено в 1768 году молодым французским математиком Жозефом Луи Лагранжем. Этот результат был официально признан только в 1882 году, после долгого и сложного доказательства.
Рациональные числа, в отличие от иррациональных, могут быть представлены в виде простой десятичной дроби или двух целых чисел, выраженных дробью. Например, число 3 - рациональное, так как его десятичное представление равно 3.000000... и повторяется бесконечно.
Интересный факт: все целые числа являются рациональными числами, так как их десятичное представление содержит только нули после десятичной запятой.
Бесконечность десятичного представления

Известно, что десятичные цифры числа π являются бесконечной последовательностью, которая не имеет определенного шаблона или правила повторения. Вместо этого, эти цифры были исследованы математиками в течение многих лет, и была разработана различная методология для вычисления и представления числа π с желаемой точностью.
Известно, что дробное представление числа π начинается с 3,14159 и продолжается бесконечно дальше, без повторения или определенного закона. Множество компьютерных алгоритмов были разработаны для нахождения более точных десятичных приближений числа π. Но даже с использованием самых мощных вычислительных машин, невозможно вычислить бесконечно точное значение числа π.
Эта неопределенность и бесконечность десятичного представления числа π придают ему свою особую магию и привлекательность в мире математики. Изучение свойств и приближений числа π является интересной и важной задачей для математиков, с теоретическими и практическими применениями в различных областях науки и инженерии.
Производные свойства
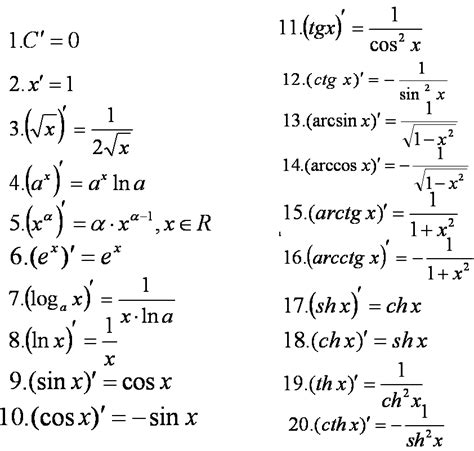
Число пи обладает несколькими интересными производными свойствами:
- Пи является бесконечной и иррациональной десятичной дробью. Это значит, что его десятичное представление не повторяется и не может быть точно выражено конечным числом цифр.
- Пи является трансцендентным числом, что означает, что оно не является корнем никакого уравнения с рациональными коэффициентами.
- Число пи является нерегулярной и беспорядочной последовательностью цифр, что делает его невозможным выразить точно с помощью обычных алгоритмов и формул.
- Пи появляется во многих математических формулах и связано с многими важными математическими константами и принципами, такими как формула Эйлера для комбинирования множественных гармонических колебаний.
- Число пи является ключевым элементом в геометрии и тригонометрии, связывая длины окружности, радиусы и углы.
Эти свойства делают число пи одним из самых загадочных и важных чисел в математике, играющим важную роль в различных науках и приложениях.
Использование в геометрии
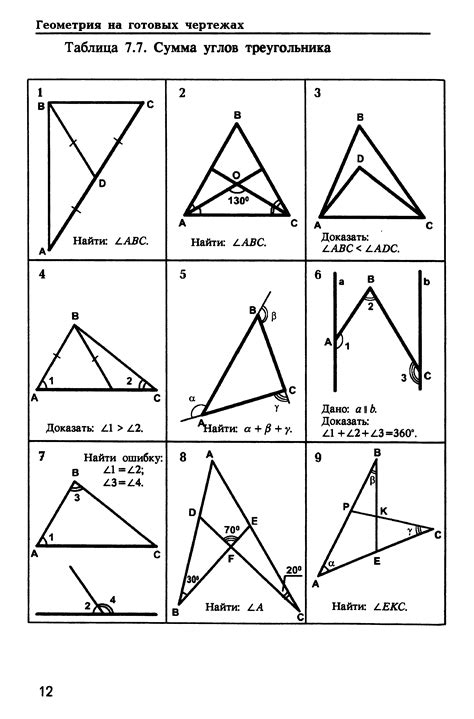
В геометрии число пи используется для расчета различных параметров круга, окружности и сферы. Например, для вычисления длины окружности можно применить формулу: L = 2πr, где L - длина окружности, r - радиус окружности.
Также число пи применяется для вычисления площади круга и сферы. Площадь круга можно найти по формуле: S = πr², где S - площадь круга, r - радиус окружности. А площадь поверхности сферы вычисляется по формуле: S = 4πr², где S - площадь поверхности сферы, r - радиус сферы.
Также число пи используется при построении геометрических фигур, таких как конусы, цилиндры и шары. Благодаря своим свойствам, пи позволяет точно определить положение и форму этих фигур.
Использование числа пи в геометрии имеет большое практическое значение. Оно помогает строить и анализировать различные фигуры и объекты, а также решать задачи связанные с геометрическими вычислениями. Поэтому знание числа пи является неотъемлемой частью математической подготовки в геометрии и других науках, где используются геометрические принципы.
Алгоритмы вычисления
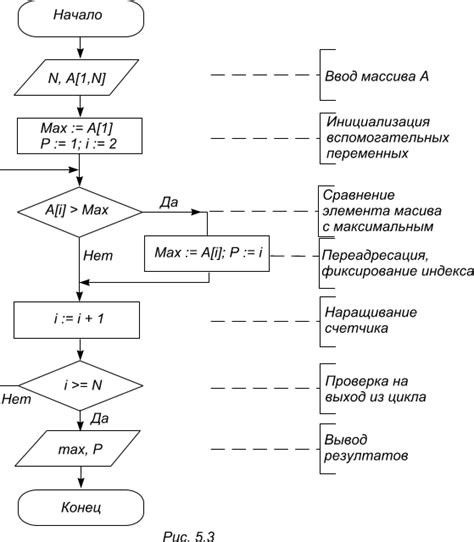
Число пи может быть вычислено различными алгоритмами, которые основаны на различных подходах и методах. Некоторые из наиболее известных алгоритмов вычисления числа пи включают:
| Алгоритм | Описание |
|---|---|
| Алгоритм Лейбница | Данный алгоритм основан на ряде Лейбница, который представляет собой сумму бесконечного ряда. Число пи вычисляется путем последовательного суммирования и вычитания долей, то есть дробей, с определенной знаковой последовательностью. |
| Алгоритм Монте-Карло | В этом алгоритме число пи вычисляется путем генерации случайных точек внутри квадрата и подсчета того, сколько из них находятся внутри единичной окружности. По мере увеличения количества генерируемых точек, полученная оценка числа пи становится более точной. |
| Алгоритм Буфона | Этот алгоритм основан на эксперименте, предложенном Буфоном. Для вычисления числа пи используется случайное бросание иглы на лист бумаги с параллельными линиями. Путем подсчета того, сколько раз игла пересекла линию, можно оценить число пи. |
| Алгоритмы, основанные на формулах | Существует множество формул, которые могут быть использованы для численного вычисления числа пи, таких как формула Мадхава-Лейбница, формула Нилаканты и формула Бейли-Боруэйна-Плаффинга. |
Каждый из этих алгоритмов имеет свои преимущества и недостатки. Выбор конкретного алгоритма зависит от требуемой точности вычислений, доступных вычислительных ресурсов и контекста, в котором числовые значения пи используются.
Значимость в науке и технике

В физике число пи используется для расчета длины окружности и площади круга, а также для изучения колебаний и волн. Оно также входит в формулы для определения объема и поверхности шара.
В инженерии и строительстве число пи является неотъемлемой частью расчетов при проектировании мостов, зданий, туннелей и других сооружений. Оно позволяет определить оптимальные размеры и формы конструкций.
В компьютерной графике и анимации число пи используется для создания реалистичных изображений и анимаций. Оно помогает определить форму объектов и точность их отображения.
В криптографии число пи используется для создания надежных алгоритмов шифрования. Оно участвует в формулах и методах для защиты информации и предотвращения несанкционированного доступа к ней.
Кроме того, число пи находит применение во многих других областях науки, таких как астрономия, космология, квантовая механика, электротехника, статистика и многие другие. Его точное значение и свойства делают его неотъемлемой частью современного научного и технического мира.



