Булевы функции, которые принимают булевы значения в качестве входных данных и возвращают булево значение, являются фундаментальными для цифровой логики. Они широко используются в компьютерных науках и электронике и, в частности, в схемотехнике.
Число булевых функций четырех переменных, то есть функций, которые принимают четыре булевых переменных в качестве входных данных, можно вычислить путем возведения двойки в степень двойки, где основание - число возможных значений каждой переменной (два), а показатель степени - число переменных.
Таким образом, число булевых функций четырех переменных равно двойке в восьмой степени, то есть 2^8 = 256. Это означает, что существует 256 возможных комбинаций значений переменных, которые могут быть входными данными для булевых функций четырех переменных.
Булевы функции четырех переменных: что это?

Булевы функции, которые принимают четыре переменные, называются функциями четырех переменных. Всего существует 16 возможных комбинаций значений для каждой из этих функций. Каждая комбинация значений переменных соответствует определенному выходному значению функции.
Преимуществом использования булевых функций четырех переменных является их выразительная сила. Они позволяют представить сложные логические операции и условия с помощью комбинаций переменных и логических операторов, таких как И (AND), ИЛИ (OR) и НЕ (NOT).
| Переменная A | Переменная B | Переменная C | Переменная D | Значение функции |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | ? |
| 0 | 0 | 0 | 1 | ? |
| 0 | 0 | 1 | 0 | ? |
| 0 | 0 | 1 | 1 | ? |
| 0 | 1 | 0 | 0 | ? |
| 0 | 1 | 0 | 1 | ? |
| 0 | 1 | 1 | 0 | ? |
| 0 | 1 | 1 | 1 | ? |
| 1 | 0 | 0 | 0 | ? |
| 1 | 0 | 0 | 1 | ? |
| 1 | 0 | 1 | 0 | ? |
| 1 | 0 | 1 | 1 | ? |
| 1 | 1 | 0 | 0 | ? |
| 1 | 1 | 0 | 1 | ? |
| 1 | 1 | 1 | 0 | ? |
| 1 | 1 | 1 | 1 | ? |
В таблице выше приведены все возможные комбинации значений переменных A, B, C и D, а также соответствующие им значения булевой функции. Знак вопроса (?) обозначает неопределенное значение, которое можно получить, зная требуемую булеву функцию.
Количество возможных комбинаций для четырех переменных
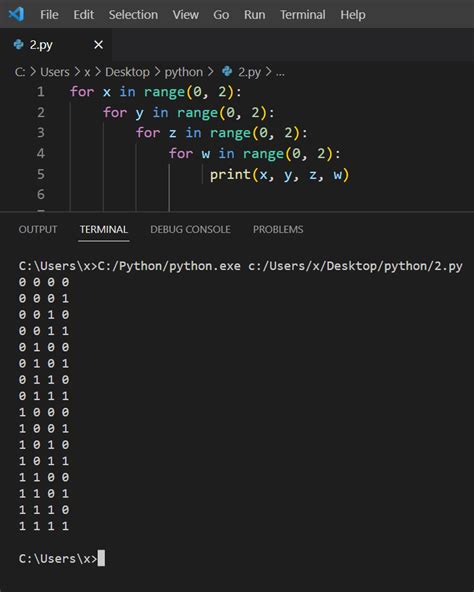
Комбинации можно представить с помощью таблицы истинности, в которой каждая строка отображает одну из возможных комбинаций. В таблице истинности для четырех переменных будет 16 строк.
Количество возможных комбинаций для булевых функций с четырьмя переменными является важной характеристикой, которая показывает разнообразие функций, которые можно создать. Каждая комбинация может соответствовать определенной логической операции, и их сочетание может создавать сложные и многофункциональные булевы функции.
Изучение числа возможных комбинаций для четырех переменных позволяет анализировать и классифицировать булевы функции, а также исследовать их свойства и возможности при создании логических схем и алгоритмов.
Примеры булевых функций четырех переменных

1. Конъюнкция (И): A ∧ B ∧ C ∧ D
2. Дизъюнкция (ИЛИ): A ∨ B ∨ C ∨ D
3. Исключающее ИЛИ (XOR): A ⊕ B ⊕ C ⊕ D
4. Полное сложение (Сумма по модулю 2): (A + B + C + D) mod 2
5. Штрих Шеффера (НЕ-И): ¬(A ∧ B ∧ C ∧ D)
6. Стрелка Пирса (НЕ-ИЛИ): ¬(A ∨ B ∨ C ∨ D)
7. Эквивалентность (Тождество): (A ⇔ B) ⇔ (C ⇔ D)
Это лишь несколько примеров возможных булевых функций четырех переменных, их комбинаций и логических связок. Комбинирование различных операций позволяет создавать более сложные и специфические функции в зависимости от требуемого результата.
Практическое применение булевых функций четырех переменных

Булевые функции четырех переменных находят широкое практическое применение в различных областях, где требуется анализ и обработка информации. Вот некоторые из примеров использования булевых функций:
- Программирование и компьютерная наука: Булевые функции играют ключевую роль в разработке программ и алгоритмов. Они используются для создания логических условий, контроля потока выполнения программы и принятия решений на основе логических операций.
- Цифровая логика и электроника: Булевые функции являются основным инструментом в проектировании и анализе цифровых систем. Они используются для создания и оптимизации схемных схем, логических вентилей и компьютерных схем, а также для описания поведения и взаимодействия цифровых компонентов.
- Криптография и защита информации: Булевые функции применяются в криптографии для шифрования данных, проверки целостности информации и защиты от несанкционированного доступа. Они способствуют созданию сложных алгоритмов, обеспечивающих безопасность и конфиденциальность при передаче и хранении информации.
- Системы искусственного интеллекта: Булевые функции используются для моделирования и решения логических задач в системах искусственного интеллекта. Они помогают компьютерам принимать решения на основе заданных правил и условий, а также анализировать и классифицировать большие объемы данных.
- Теория вероятностей и статистика: Булевые функции являются важной частью анализа данных и моделирования случайных событий. Они используются для формализации и описания логических условий, а также для выражения и исследования вероятностных зависимостей и статистических свойств данных.
Это лишь некоторые примеры практического применения булевых функций четырех переменных. Их универсальность и гибкость открывают широкий спектр возможностей в области анализа, моделирования и принятия решений на основе логических операций.
Конечный результат: число булевых функций четырех переменных

Каждая из этих 65536 функций может быть выражена с помощью логических операций И (AND), ИЛИ (OR) и НЕ (NOT) над четырьмя переменными. Некоторые из этих функций могут быть простыми и выразимыми одними операциями, а некоторые могут быть более сложными и требовать несколько операций для выражения.
Число булевых функций четырех переменных является очень большим, и исследование всех этих функций является сложной задачей. Тем не менее, изучение свойств и особенностей различных классов булевых функций, а также их применение в различных областях, является важной задачей в теории и практике компьютерной науки.



