Математика состоит из множества понятий, имеющих свои специфичные определения. Одно из таких понятий - кратность чисел. Число, кратное другому числу, является основой многих математических операций и имеет важное значение в различных областях науки.
Определение кратности чисел заключается в следующем: число \(a\) называется кратным числа \(b\), если оно делится на \(b\) без остатка. Иными словами, \(b\) является делителем числа \(a\). Например, число 15 кратно числу 3, потому что \(15 = 3 \times 5\), и деление отсутствует. Если же остаток от деления равен нулю, то \(a\) делится на \(b\) детерминировано и абсолютно.
Кратные числа могут быть использованы во множестве практических ситуаций. Например, когда нужно разделить количество предметов на определенное количество групп, корзин или ящиков. В таких случаях кратные числа помогают упростить задачу и позволяют равномерно распределить элементы.
Что такое кратное число?

Например, число 15 является кратным числа 3, потому что оно делится на 3 без остатка: 15 ÷ 3 = 5. 15 также является кратным числа 5, 15 ÷ 5 = 3. Однако число 15 не является кратным числа 4, потому что при делении 15 на 4 получится остаток 3.
Кратные числа могут быть положительными и отрицательными. Например, -12 является кратным чисел 2, -4 и 12.
Чтобы определить, является ли число кратным другому числу, мы можем воспользоваться определением кратности и выполнить деление чисел. Если остаток от деления равен нулю, то число является кратным, если остаток не равен нулю, то число не является кратным.
Методы определения кратности чисел

| Метод | Описание |
|---|---|
| Деление нацело | В этом методе число делится на другое число, и если остаток от деления равен нулю, то число является кратным. |
| Умножение | Если одно число можно получить путем умножения другого числа на целое число, то они являются кратными. |
| Проверка последних цифр | Если последние цифры двух чисел совпадают, то они могут быть кратными. |
| Сложение и вычитание | Если при сложении или вычитании чисел получается кратное число, то они являются кратными. |
Использование соответствующего метода зависит от конкретной ситуации и удобства для определения кратности чисел. Важно помнить, что кратность чисел имеет важное значение во многих математических и практических задачах, и понимание методов определения кратности помогает в их решении.
Кратность и деление нацело
Кратность числа определяет, сколько раз одно число является делителем другого числа без остатка. Например, число 15 кратно числу 3, так как 15 делится на 3 без остатка (15:3=5).
Деление нацело - это процесс разделения одного числа на другое таким образом, чтобы результат был целым числом и не оставался остатка. Например, при делении числа 10 на число 2 без остатка, получаем результат 5 (10:2=5).
Чтобы проверить кратность числа, мы можем воспользоваться делением нацело. Если результат деления двух чисел равен целому числу, значит, число является кратным.
Для наглядного представления кратности числа, можно использовать таблицу. В таблице мы можем указать число, на которое проверяем кратность, и отметить все числа, кратные данному числу.
| Число | Кратные числа |
|---|---|
| 2 | 2, 4, 6, 8, 10, ... |
| 3 | 3, 6, 9, 12, 15, ... |
| 4 | 4, 8, 12, 16, 20, ... |
Таким образом, кратность числа и деление нацело помогают нам понять, какие числа делятся на другие числа без остатка. Эти понятия широко используются в математике и имеют применение в различных областях науки и повседневной жизни.
Особенности кратных чисел
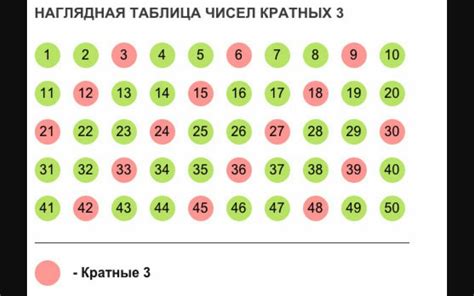
Особенности кратных чисел:
1. Свойство делимости: Если число A кратно числу B, то A можно представить в виде произведения числа B на некоторое целое число C. То есть A = B * C.
2. Бесконечное множество кратных чисел: Если число A кратно числу B, то любое число, кратное A, также будет кратным числу B. Таким образом, существует бесконечное множество кратных чисел для каждого числа.
3. Отношение "деление без остатка": Кратное число является конкретным примером отношения "деление без остатка". Если число A кратно числу B, то A/B - это целое число без остатка.
4. Кратные числа в арифметике: Кратные числа используются для решения задач арифметики, например, для нахождения наименьшего общего кратного (НОК) двух или нескольких чисел.
5. Кратные числа в учете и экономике: Кратные числа используются для упрощения расчетов в учетно-экономической сфере. Например, в бухгалтерии используется кратность определенной валюты или ставки налога.
Знание особенностей кратных чисел позволяет более глубоко понять и использовать их в различных областях науки и повседневной жизни.
Примеры кратных чисел

1. Кратные числа 2 и 4: число 8 является кратным числам 2 и 4, так как 8 делится без остатка на 2 и на 4.
2. Кратные числа 5 и 10: число 30 является кратным числам 5 и 10, так как 30 делится без остатка на 5 и на 10.
3. Кратные числа 3 и 6: число 18 является кратным числам 3 и 6, так как 18 делится без остатка на 3 и на 6.
4. Кратные числа 9 и 12: число 36 является кратным числам 9 и 12, так как 36 делится без остатка на 9 и на 12.
Таким образом, кратные числа играют важную роль в математике и в реальной жизни. Они помогают в решении задач, а также используются в различных научных и технических областях.
Практическое применение кратности чисел

В финансовой сфере применение кратности чисел может быть связано с расчетом процентов или долей. Например, если мы хотим поделить некую сумму денег поровну на определенное количество людей, нам важно знать, является ли эта сумма кратной количеству людей. Иначе нам придется разбивать сумму на неравные доли, что может вызвать неудовлетворение или конфликт.
В программировании знание кратности чисел также является важным. Например, при работе с циклами, мы можем использовать понятие кратности для выполнения определенных действий. Если нужно обработать только числа, кратные или не кратные определенному числу, мы можем использовать условные операторы, чтобы выбрать нужные значения.
Понятие кратности также используется в науке, в частности при изучении частоты и равномерности явлений. Например, в физике при изучении световых волн или в биологии при анализе генетических связей. Знание кратности чисел позволяет лучше понять и описать закономерности и поведение этих систем.
Таким образом, практическое применение кратности чисел весьма широко и находит свое место в различных научных и практических областях. Понимание и использование этого понятия помогает упростить решение задач и легче описывать мир вокруг нас.
Значение кратных чисел в математике и науке
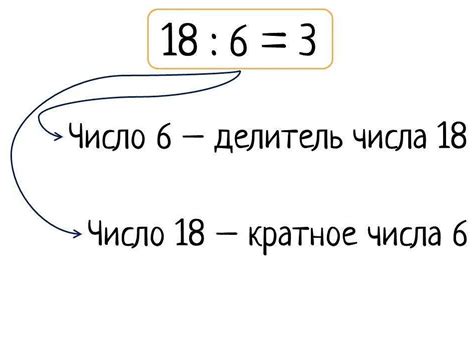
Кратные числа играют важную роль в математике и науке. Они представляют собой числа, которые могут быть делены на другое число без остатка. Такие числа часто встречаются в различных областях и имеют свои особенности и свойства.
Кратные числа используются в различных областях математики, таких как алгебра, теория чисел и геометрия. Например, в алгебре кратные числа используются для решения уравнений и систем уравнений. В теории чисел они играют важную роль при изучении свойств числовых последовательностей и числовых систем. В геометрии кратные числа могут использоваться для определения определенных свойств фигур и формул.
В науке кратные числа также имеют большое значение. Например, в физике они могут использоваться для измерения времени, скорости, частоты и других физических величин. В химии кратные числа могут использоваться для определения соотношения между массой и количеством вещества в химической реакции.
Кроме того, кратные числа могут быть использованы для решения различных практических задач. Например, они могут быть использованы для вычисления результата во время деления, для определения времени при расчете срока действия некоторых событий или для определения количества элементов в группе или ансамбле.
Итак, кратные числа имеют большое значение в математике и науке. Они позволяют решать различные задачи, описывать и изучать свойства чисел и применять их в различных областях. Понимание и использование кратных чисел является важным навыком и может быть полезным во многих ситуациях.
Как использовать кратность чисел для упрощения расчетов

Понятие кратности чисел широко используется в математике и арифметических операциях. Кратность числа позволяет упростить расчеты и найти ряд закономерностей в числовых последовательностях.
Основным принципом кратности является возможность деления одного числа на другое без остатка. Если число А делится на число В без остатка, то А является кратным числом В.
Рассмотрим пример: число 15 кратно числу 3, так как 15 делится на 3 без остатка. Деление 15 на 3 равно 5. Также, число 15 кратно числу 5, так как 15 делится на 5 без остатка. Деление 15 на 5 также равно 3.
Кратность чисел позволяет быстро находить общие делители двух или более чисел. Например, числа 12 и 24 оба кратны числу 3. Так как деление 12 на 3 равно 4, а деление 24 на 3 равно 8, то оба числа можно представить как произведение 3 на натуральные числа 4 и 8.
Кратность чисел также важна при решении задач и упрощении уравнений. Зная кратность чисел, можно повторять операции с числами, пропуская некоторые шаги вычислений и получая точные результаты более эффективно. Например, при упрощении выражения 9x + 6x, можно сократить наименьший общий множитель чисел 9 и 6, получив 3(3x + 2x), что равно 15x.
Кратность чисел пригодна для решения разнообразных задач на практике. В области финансов, налогообложения и скидок, кратность чисел используется для упрощения расчетов и округления сумм. Кратность также применяется в науках и технике при решении физических задач и проектировании структур.



