(а - b) в квадрате – это математическое выражение, которое означает возведение разности чисел а и b в квадрат. Эта формула широко используется в различных областях науки и техники, включая физику, статистику, программирование и многие другие.
Формула для расчета (а - b) в квадрате выглядит следующим образом: (а - b)2. Для выполнения расчетов нужно вычислить разность чисел а и b, а затем возвести эту разность в квадрат. Получившееся число будет являться результатом данного выражения.
Значение выражения (а - b) в квадрате может быть как положительным, так и отрицательным, в зависимости от значений a и b. Например, если a = 5 и b = 3, то (5 - 3)2 = 4. Если же a = 3 и b = 5, то (3 - 5)2 = 4. Таким образом, расчеты следует проводить внимательно, чтобы избежать возможных ошибок.
Формула для расчета числа (а - b) в квадрате
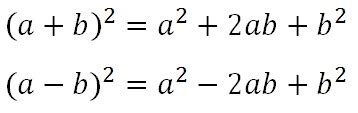
| (а - b) в квадрате = а в квадрате - 2аб + b в квадрате |
Где:
- а - это исходное число, из которого нужно вычесть число b;
- b - это число, которое нужно вычесть из числа а;
- а в квадрате - это а, умноженное на само себя;
- 2аб - это результат умножения числа а на число b, умноженного на 2;
- b в квадрате - это b, умноженное на само себя.
Подставив в формулу значения чисел а и b, мы можем вычислить (а - b) в квадрате. Например, если а = 5, а b = 2, то:
| (5 - 2) в квадрате = 5 в квадрате - 2 * 5 * 2 + 2 в квадрате |
| (5 - 2) в квадрате = 25 - 20 + 4 |
| (5 - 2) в квадрате = 9 |
Таким образом, число (5 - 2) в квадрате равно 9.
Какие значения можно получить при расчете числа (а - b) в квадрате
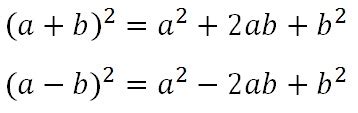
- Если значения а и b равны, то получится квадрат разности a-b. Например, если а=2 и b=2, то (а - b) в квадрате будет равно 0.
- Если значение а больше значения b, то получится положительный квадрат разности a-b. Например, если а=5 и b=2, то (а - b) в квадрате будет равно 9.
- Если значение b больше значения a, то получится отрицательный квадрат разности a-b. Например, если а=2 и b=5, то (а - b) в квадрате будет равно -9.
В общем случае, при расчете числа (а - b) в квадрате, получится квадрат разности a-b.
Выбор чисел а и b для расчета
Чтобы получить положительный результат, в большинстве случаев рекомендуется выбирать числа а и b таким образом, чтобы а было больше, чем b.
Если задача требует получить отрицательное значение, то числа а и b могут быть любыми, главное, чтобы а было меньше, чем b.
Выбор чисел а и b также может зависеть от условий задачи и конкретной математической модели, которую используете.
При выборе чисел а и b следует учитывать, что результат расчета (а - b) в квадрате может быть нулевым или отрицательным числом, в зависимости от выбора значений.
Перед выбором чисел а и b желательно приступить к анализу задачи и определить, какие значения переменных будут наиболее подходящими для данной ситуации.
Как рассчитывать число (а - b) в квадрате
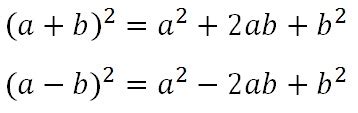
- Возьмите значение числа a и вычтите из него значение числа b. Полученное число обозначим как c = a - b.
- Возьмите значение числа c и умножьте его на само себя (возводите в квадрат). Полученный результат обозначим как d = c * c.
Таким образом, число (а - b) в квадрате будет равно значению числа d.
Например, если даны числа a = 5 и b = 3, то:
- Вычитаем из числа а значение числа b: c = 5 - 3 = 2.
- Возводим значение числа c в квадрат: d = 2 * 2 = 4.
Таким образом, число (5 - 3) в квадрате равно 4.
Теперь вы знаете, как рассчитать число (а - b) в квадрате! Это простая формула, которая может пригодиться в различных задачах, связанных с математикой или программированием.
Использование числа (а - b) в квадрате в математических выражениях

Часто в задачах возникают ситуации, когда нужно найти разность квадратов двух чисел. В таких случаях формула (а - b)^2 приходит на помощь. Например, при расчете площади прямоугольника, где одна сторона равна (а - b) и другая сторона равна (а + b), можно воспользоваться формулой (а - b)^2.
Важно отметить, что (а - b) в квадрате можно представить в различных вариантах. Например, если (а - b) = 5, то (а - b)^2 = 25. Если (а - b) = -3, то (а - b)^2 = 9. Таким образом, значение (а - b) влияет на итоговый результат.
Использование числа (а - b) в квадрате в математических выражениях может помочь в решении задач из различных областей, таких как алгебра, геометрия, физика и др. Эта формула является одним из базовых инструментов математического анализа и помогает упростить вычисления и решение задач.
Какие применения может иметь число (а - b) в квадрате
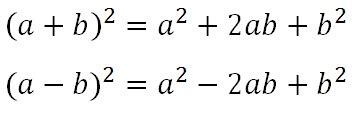
Ниже приведены некоторые примеры применения этой формулы:
| Пример применения | Описание |
|---|---|
| Вычисление площади разности двух прямоугольников | Если имеется два прямоугольника с сторонами a и b, то их разность в квадрате (a - b)^2 может быть использована для вычисления площади области, ограниченной внешними границами первого прямоугольника и внутренними границами второго прямоугольника. |
| Нахождение расстояния между двумя точками на координатной плоскости | Если имеются две точки с координатами (x1, y1) и (x2, y2), то расстояние между ними может быть вычислено с помощью формулы разности квадратов (x2 - x1)^2 + (y2 - y1)^2. |
| Определение точки пересечения графиков функций | Если заданы две функции f(x) и g(x), то точка их пересечения может быть найдена с помощью решения уравнения (f(x) - g(x))^2 = 0. Это позволяет найти значения x, при которых графики функций пересекаются. |
Формула разности квадратов (а - b) в квадрате является мощным инструментом, позволяющим решать различные задачи и выполнять расчеты в разнообразных областях.
Часто задаваемые вопросы о числе (а - b) в квадрате
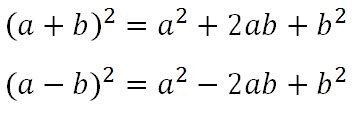
| Вопрос | Ответ |
|---|---|
| Что такое число (а - b) в квадрате? | Число (а - b) в квадрате - это результат умножения разности чисел а и b на себя. Формула для вычисления такого числа выглядит следующим образом: (а - b)². |
| Как вычислить число (а - b) в квадрате? | Чтобы вычислить число (а - b) в квадрате, нужно вычислить разность чисел а и b, а затем возвести эту разность в квадрат. Например, если а = 5 и b = 3, то (а - b) в квадрате будет равно (5 - 3)² = 2² = 4. |
| Какие значения может принимать число (а - b) в квадрате? | Число (а - b) в квадрате может принимать любые неотрицательные значения. Это связано с тем, что квадрат любого числа всегда положителен или равен нулю. Таким образом, результатом вычисления (а - b) в квадрате всегда будет неотрицательное число или ноль. |
| Зачем нужно вычислять число (а - b) в квадрате? | Вычисление числа (а - b) в квадрате имеет ряд практических применений. Например, оно может использоваться для решения математических задач, моделирования физических процессов, анализа данных и других задач, где требуется работы с разностями чисел и их возведением в квадрат. |



