Двоичная система счисления является основной системой компьютеров, в которой числа представляются с помощью двух цифр - 0 и 1. В этой системе символ 0 обозначает отсутствие, а символ 1 - наличие. А что происходит, если нам нужно преобразовать число из двоичной системы счисления в десятичную?
Для выполнения такого преобразования мы должны разложить число на отдельные разряды и умножить каждый разряд на соответствующую степень числа 2. Возьмем, например, число 10101. Оно состоит из пяти разрядов, каждый из которых принимает значение 0 или 1.
Проведя преобразование, получим: 1 * 2^4 + 0 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 16 + 0 + 4 + 0 + 1 = 21. Таким образом, число 10101 в двоичной системе счисления равно 21 в десятичной системе.
01 в двоичной системе счисления
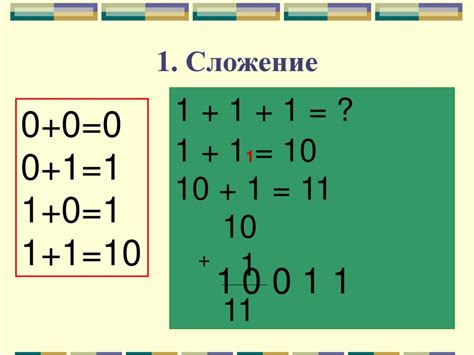
В десятичной системе счисления число 01 эквивалентно числу 1. Оно имеет значение, равное 1, так как умножение числа 1 на 10 в степени 0 даёт 1.
Числа в двоичной системе
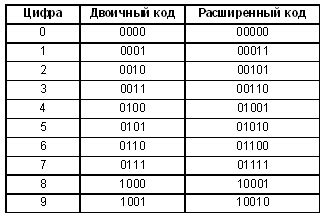
Чтобы преобразовать число из двоичной системы в десятичную систему, необходимо умножить каждую цифру числа на соответствующую ей степень двойки и сложить полученные произведения. Например, число 10101 в двоичной системе можно преобразовать в десятичную систему следующим образом:
| Позиция | Степень двойки | Цифра | Произведение |
|---|---|---|---|
| 4 | 16 | 1 | 16 |
| 3 | 8 | 0 | 0 |
| 2 | 4 | 1 | 4 |
| 1 | 2 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| Сумма | 21 | ||
Таким образом, число 10101 в двоичной системе равно 21 в десятичной системе.
Понятие двоичной системы счисления

Двоичная система счисления широко используется в современных компьютерных технологиях, так как это естественный способ представления чисел в электронных устройствах. Каждая цифра двоичной системы, называемая битом (от английского binary digit), является минимальной единицей информации и может принимать только два значения.
Для преобразования чисел из двоичной системы счисления в десятичную используется позиционный принцип. Каждая цифра числа в двоичной системе имеет вес, который зависит от ее позиции. Преобразование осуществляется путем умножения каждого разряда числа на соответствующий ему вес и последующего сложения результатов.
| Разряд | 8 | 4 | 2 | 1 |
|---|---|---|---|---|
| Значение | 1 | 0 | 1 | 0 |
| Вес | 23 | 22 | 21 | 20 |
| Результат | 8 | 0 | 2 | 0 |
Таким образом, число 10102 в двоичной системе счисления эквивалентно числу 1010 в десятичной системе счисления.
Преобразование числа 10101 в десятичную систему

Для преобразования числа 10101 из двоичной системы в десятичную систему, необходимо умножить каждую цифру числа на 2 в степени соответствующего разряда числа, начиная справа. Затем сложить полученные результаты.
Для числа 10101:
1 * 2^4 + 0 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 16 + 0 + 4 + 0 + 1 = 21
Таким образом, число 10101 в двоичной системе счисления равно 21 в десятичной системе счисления.
Алгоритм преобразования
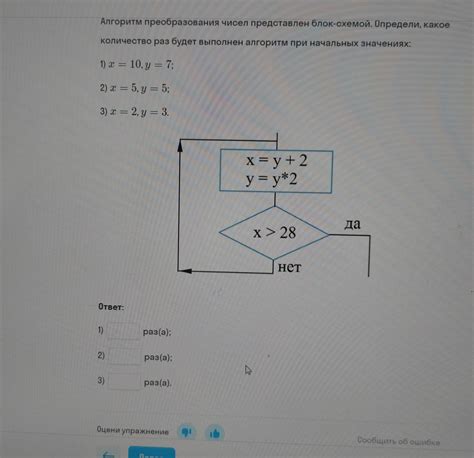
Для преобразования числа 10101 из двоичной системы счисления в десятичную систему необходимо выполнить следующие шаги:
- Разбить число на разряды, начиная с младшего разряда. В данном случае число 10101 разбивается на разряды: 1, 0, 1, 0, 1.
- Умножить каждый разряд числа на соответствующую степень числа 2. В данном случае умножение будет следующим: 1x2^4 + 0x2^3 + 1x2^2 + 0x2^1 + 1x2^0.
- Выполнить умножения и сложения по правилам алгебры: 1x2^4 + 0x2^3 + 1x2^2 + 0x2^1 + 1x2^0 = 16 + 0 + 4 + 0 + 1 = 21.
Таким образом, число 10101 в двоичной системе счисления равно числу 21 в десятичной системе счисления.
| Разряд | Значение | Степень 2 | Умножение |
|---|---|---|---|
| 4 | 1 | 2^4 | 1x2^4 |
| 3 | 0 | 2^3 | 0x2^3 |
| 2 | 1 | 2^2 | 1x2^2 |
| 1 | 0 | 2^1 | 0x2^1 |
| 0 | 1 | 2^0 | 1x2^0 |



