Центральный и вписанный угол – два важных понятия, связанных с окружностями. Окружность – это геометрическая фигура, состоящая из всех точек, равноудаленных от центра. Центральный угол – это угол, в вершине которого находится центр окружности.
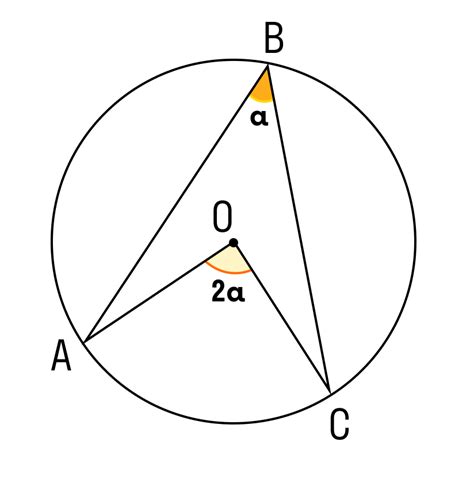
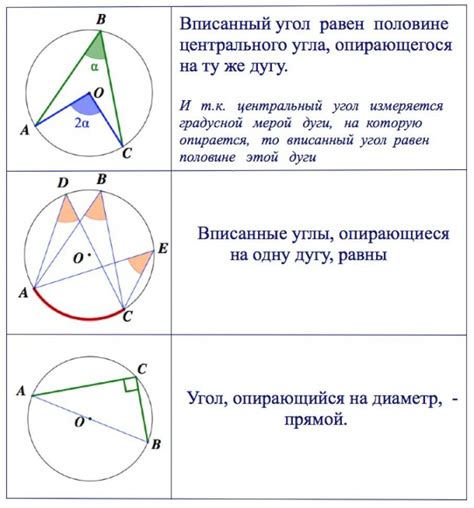
В данном случае, стоит отметить замечательное свойство: центральный угол равен вписанному углу, опирающемуся на ту же дугу окружности. Таким образом, если на окружности даны две точки, их соединяющая дуга будет образовывать центральный и вписанный угол.
Известно, что сумма всех углов в любом треугольнике равна 180 градусов. В случае равностороннего треугольника, каждый угол будет составлять 60 градусов. В треугольнике, вписанном в окружность, один из углов будет равняться половине центрального угла. Следовательно, в данной ситуации вписанный угол будет составлять 30 градусов.
Таким образом, центральный и вписанный угол окружности имеют тесную связь друг с другом. Зная размер центрального угла (измеряемый в градусах), можно легко определить величину вписанного угла, используя соответствующее свойство равенства. Эти понятия полезны в геометрии, строительстве, физике и других областях науки.
Идеальные формы геометрии
Одной из таких идеальных форм является окружность. Это плоская фигура, представляющая собой множество точек, равноудаленных от центра. Центральный угол окружности – это угол, образованный двумя лучами, исходящими из центра окружности и проходящими через две ее точки. Вспоминаем школьный курс геометрии: такой угол равен сумме вписанных углов, образованных двумя лучами, выходящими из одной точки на окружности и пересекающими дугу окружности.
Вписанный угол окружности – это угол, образованный двумя лучами, пересекающими дугу окружности из одной точки. Это угол, который лежит внутри окружности и вдоль ее дуги. Вписанный угол всегда половину центрального угла, охватывающего ту же дугу. Такая геометрическая связь между центральным и вписанным углами окружности является одной из фундаментальных особенностей этой идеальной формы.
Центральный угол окружности: определение и свойства
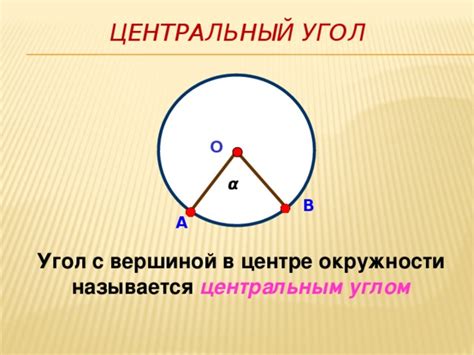
Центральный угол в окружности определяется двумя лучами, которые имеют общий начальный пункт в центре окружности. Угол измеряется в градусах или радианах и его величина соответствует дуге между этими лучами на окружности.
Свойства центрального угла в окружности:
1. Центральный угол всегда равен половине центральной дуги, перекрываемой этим углом. Если центральная дуга равна 360 градусам (полный оборот), то центральный угол также равен 360 градусам.
2. Все центральные углы, опирающиеся на одну и ту же центральную дугу, равны между собой.
3. Если два центральных угла имеют одинаковую величину, то и их опрашиваемые дуги также равны.
4. Сумма центральных углов, опирающихся на одну и ту же центральную дугу, равна 360 градусам (полному обороту).
5. Центральный угол, опирающийся на половину окружности, будет равен 180 градусам. Такой угол называется прямым углом.
Центральные углы являются важными понятиями в геометрии окружности и широко применяются для изучения свойств исследуемых фигур. Понимание этих свойств поможет лучше воспринимать и анализировать геометрические конструкции, основанные на окружностях и их частях.
Центральный угол окружности: формула для расчета
Для расчета центрального угла окружности необходимо знать длину хорды или длину дуги, а также радиус окружности.
Формула для расчета центрального угла задается следующим образом:
Угол (в радианах) = (Длина хорды или длина дуги) / Радиус
Угол (в градусах) = (Длина хорды или длина дуги) * (180 / π) / Радиус
Здесь π - математическая константа, приближенно равная 3.14159.
Вписанный угол окружности: определение и свойства
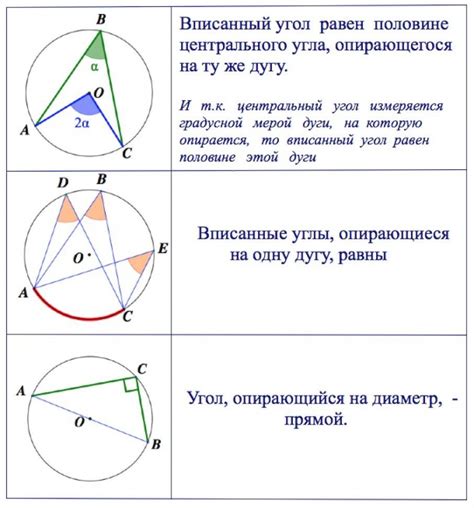
Опирающиеся на одну дугу окружности, вписанные углы равны между собой. Если две окружности пересекаются в двух точках, то их вписанные углы также равны.
У вписанных углов имеются также следующие свойства:
- Вписанный угол является половинным углом дуги, на которую он опирается. То есть, если дуга окружности угла равна α градусов, то сам вписанный угол будет равен α/2 градусов.
- Вписанный угол окружности, опирающийся на ту же дугу, что и сентральный угол, будет в два раза меньше сентрального угла.
- Сумма двух вписанных углов на окружности будет равна 180 градусов.
- Внешний угол вписанного угла окружности будет равен разности 180° – α/2, где α – мера вписанного угла.
- Угол, образованный касательной к окружности и хордой, равен вписанному углу, который опирается на ту же хорду.
Вписанный угол окружности – одно из основных понятий геометрии окружности, которое широко применяется в различных геометрических задачах и конструкциях.
Вписанный угол окружности: формула для расчета
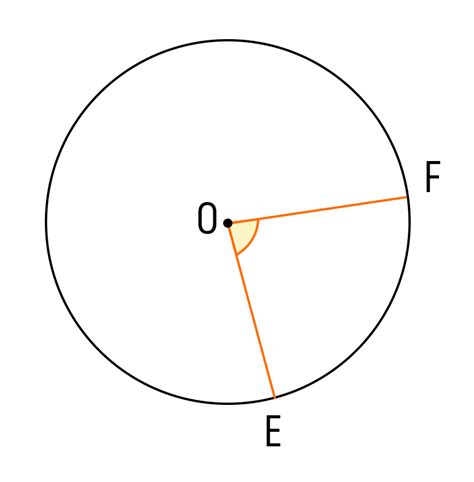
Для расчета вписанного угла окружности существует формула:
Вписанный угол = 1/2 * мера дуги
Здесь "мера дуги" обозначает длину дуги окружности, измеряемую в градусах или радианах.
Эту формулу можно применить для нахождения вписанных углов окружности в различных задачах, например, при определении значения угла, образованного хордой, или при поиске измерения вписанного угла в центральном угле, опирающемся на ту же дугу.
Различия между центральным и вписанным углами окружности

Центральный угол:
Центральный угол - это угол с вершиной в центре окружности, который заключает в себе дугу окружности. Он измеряется в градусах и может быть любого размера от 0 до 360 градусов.
Основные характеристики центрального угла:
- Центральный угол всегда равен половине своей соответствующей дуги.
- Центральный угол и его соответствующая дуга имеют одинаковую меру (в градусах).
- Если центральный угол равен 180 градусам, то соответствующая дуга является диаметром окружности.
Вписанный угол:
Вписанный угол - это угол с вершиной на окружности, который заключает в себе дугу окружности. Он также измеряется в градусах, но его размер ограничен от 0 до 180 градусов.
Основные характеристики вписанного угла:
- Вписанный угол всегда равен половине его соответствующей дуги.
- Вписанный угол и его соответствующая дуга имеют одинаковую меру (в градусах).
- Если вписанный угол равен 180 градусам, то соответствующая дуга является полной окружностью.
Таким образом, различия между центральным и вписанным углами заключаются в их измерении и ограничениях: центральный угол может быть от 0 до 360 градусов, в то время как вписанный угол может быть от 0 до 180 градусов. Оба угла имеют одинаковую соответствующую дугу и равны половине ее меры.
Практические примеры использования центральных и вписанных углов окружности
Центральные и вписанные углы окружности широко используются в различных областях. Рассмотрим несколько практических примеров их применения:
1. Геометрия
Центральные и вписанные углы часто встречаются в геометрии. Они позволяют решать различные задачи, связанные с окружностями. Например, центральный угол может использоваться для определения длины дуги окружности по известному радиусу и центральному углу. Вписанный угол помогает определить центр окружности по известным точкам, лежащим на этой окружности.
2. Архитектура
Центральные и вписанные углы окружности также активно применяются в архитектуре. Например, при создании круговых залов или куполов архитекторы используют центральные углы для определения геометрических параметров построений. Вписанные углы могут использоваться для создания красивых и симметричных архитектурных элементов.
3. Физика
Центральные и вписанные углы окружности имеют свои применения и в физике. Например, в механике они используются при изучении движения твердых тел по окружности. Центральный угол может быть использован для вычисления радиуса, скорости и угловой скорости тела. Вписанный угол позволяет определить траекторию движения тела и его ускорение.
Во всех этих примерах понимание центральных и вписанных углов окружности играет важную роль в решении различных задач и создании эффективных конструкций.



